Inscription / Connexion Nouveau Sujet
Derivation
Bonjour j'ai un dm de math a rendre pour mercredi et je viens de m'en apercevoir étant donné que mon professeur l'a mis en ligne que ce week-end
Merci d'avance pour votre gentillesse de bien vouloir m'aider sur ce sujet
Les questions sont avec le document attaché
Merci 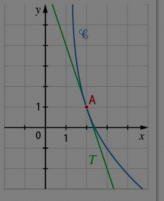
* malou > si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum. *![]() Sujet ancien- ne plus donner ce lien-merci
Sujet ancien- ne plus donner ce lien-merci
Haha non mais sérieusement il aurait pu nous prévenir avant les vacances qu'il mettrait un devoir sur pronote au lieu de nous afficher ca par surprise
Ah oui désolé elles étaient dans la photo mais ça n'a pas marcher :
1) Determiner g'(2) par lecture graphique
2) Calculer g'(x) puis en déduire g'(2)
3) Reproduire la courbe C de la fonction g puis tracer sa tengente au point d'abscisse 3
4.a) Vérifiez que pour tout réel x de I g(x)=-x+1+(2÷(x-1)
4.b) Calculer g'(x) en utilisant cette expression
Vérifiez la cohérence des réponses apportées à la question 2
5.a) Montrer que T a pour equation réduite y=-3x+7
5.b) Demontrer que C est au dessus de T sur I
Et tu réponds quoi, à la question 1 ?
Pour la suite, il faudrait mettre l'énoncé ... Il en manque !!!
1) g'(2) est la pente de la tangente au point d'abscisse 2.
Pour la suite, donner l'expression de g(x) avant de montrer ton travail.
Et tu réponds quoi, à la question 1 ?
Pour la suite, il faudrait mettre l'énoncé ... Il en manque !!!
Soit g la fonction définie sur l'intervalle I=]1;+~[ par g(x)= (-x²+2x+1)÷(x-1)


