Pour la 1)
J'ai dit qu'il y a un erreur dans l'intervalle car
L'ensemble de définition de cette fonction est ]-;-][;+[
Donc il est dérivable par conséquent sur cette intervalle

non !

et de plus une réunion d'intervalles n'est pas forcément un intervalle !

Bonsoir ;
Est ce que mon réponse à la première question est faux ?
S'il est faux je veux une petite indications s'il vous plaît et merci beaucoup d'avance

je ne vois aucune question résolue et justifiée !

la fonction racine est définie sur [0 : + inf[ et dérivable sur ]0 ; + inf[

c'est une fonction de référence...

Bonsoir ;
Pour la 2)
f'(x)=()=

Bonjour ;

Est ce qu'il y a une réponse ?

salut, oui c'est juste

Bonjour ;
Merci beaucoup de m'avoir répondu !
Mais ma réponse à la première question est ce que c'est juste ?

si u est strictement positive et derivable sur un intervalle I alors racine de u est derivable sur I
ici f est derivable sur ]-inf;sqrt(2)[ et sur ]sqrt(2);inf[

Bonjour
Merci beaucoup à vous !
Donc on a f est strictement positive et dérivable sur
]-;-[];+[ [d'après sont ensemble de définition (il est fermé en \sqrt 2 et -\sqrt 2 ) mais en dérivation non il est ouvert sur cette intervalle (c.à d) il est strictement positive sur \sqrt 2 et strictement négatif sur -\sqrt 2

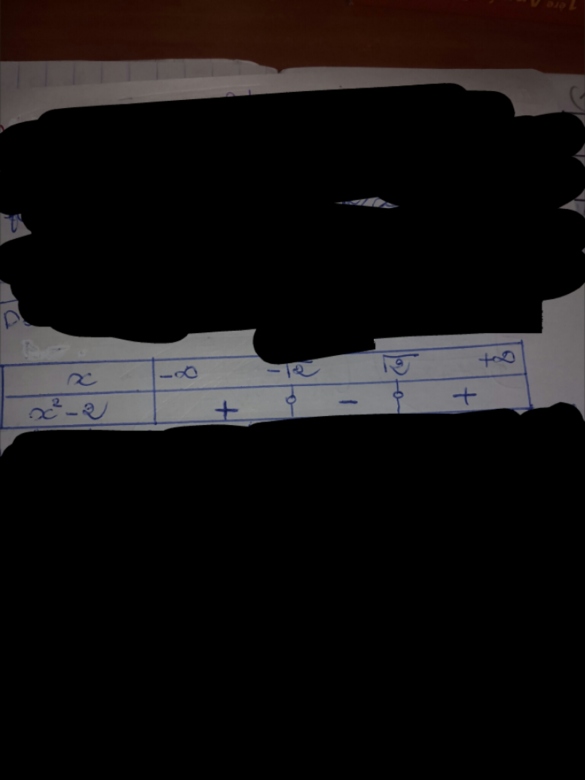
x->x^2-2 est strictement positive, derivable sur ]-inf;-sqrt(2)[ et sur ]sqrt(2);inf[
donc x->sqrt(x^2-2) est derivable sur ]-inf;-sqrt(2)[ et sur ]sqrt(2);inf[
mais l'ensemble de derivabilite pourrait etre plus grand, il faudrait etudier la derivabilite en -sqrt(2) et en sqrt(2), ce qui n'est pas demande ici

Bonjour ;
Erreur de ma part ;
f est dérivable et strictement positive sur
]-;-[et ];+[
Car si en fait le tableau de signe ;

c'est l'interieur de la racine qui est strictement positif (pour appliquer le th)
le reste est correct me semble-t-il