Inscription / Connexion Nouveau Sujet
Dérivation
Besoin d'aide pour mon exo
Répondre par vrai ou faux
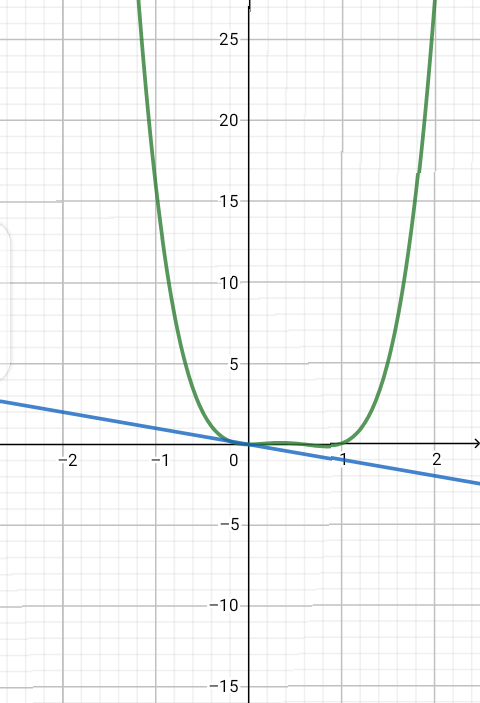
1-Soit f(x)=x³(-x+1)² definie sur R. Cf sa courbe représentative .Alors :
a- f'(x)=x²(1-x)(5-3x).
b- f'(0)=0
c-f change de sens de variation en 0
d- f s'annule en x=1/2
d-La courbe de f a trois tangentes horizontales
e- Il existe plus d'une tangente à Cf parallèle à la droite (y=-x)
f) f(-101000)>f(-101001)
g-Pour tout réel x , f(x)≤ f(3/5)
1-
f'(x)=x²(1-x)(5-3x) Vrai
f'(x)=3x²(-x+1)²+2x³(x-1)
=x²[3(1-2x+x²)+2x(x-1)]
=x²[3-6x+3x²+2x²-2x]
=x²(5x²-8x+3)
=x²(5x²-3x-5x+3)
=x²(5x²-3x-(5x-3))
=x²(x(5x-3)-(5x-3))
=x²((5x-3)(x-1))
f'(x)=x²((3-5x)(1-x))
b) f'(0)=0 vrai
c) Vrai , f'(0)=0 ,donc Cf admet une tangente horizontale en 0 , et f' s'annule en changeant de signe en 0, par suite f change de sens de variation en 0
d)
f'(0)=0 <=> x²(1-x)(5-3x)
<=> x²=0 ou x=1 ou x=5/3
Donc f' ne s'annule pas en 1/2
La courbe de f a 3 tangentes horizontales: Vrai
Il faut factoriser d'abord au lieu de développer vous pouviez mettre aussi en facteur
On change les signes des deux parenthèses si vous voulez retrouver la forme donnée
Ensuite b) et c)
C faux certes une tangente horizontale mais f'(x) ne change pas de signe elle reste croissante
D Il ne faut pas prendre leur dérivée fausse mais la votre
Il y a encore 2 D
D_2 oui 3 tangentes parallèles à l'axe des abscisses
Donc b-Vra
c)Faux
d) f'(x)=0 <=> x=0 ou x=1 ou x=3/5
Donc faux
La courbe admet trois tangentes horizontales: vrai
e)
Quand je fais
f'(x)=-1 <=> 5x⁴-3x³-2x²+1=0
J'arrive pas à resoudre
La droite bleue tracée, ce n'est pas l'équation y = -1 ! (mais plutôt y = -x...)
Elle est sensée être horizontale...
On demande l'intersection de la courbe f' avec la droite y = -1.
En effet, il n'y a aucune intersection, donc f'(x) = -1 n'admet pas de solution.
La dérivée s'annule en changeant de signe
en 0 pas de changement de signe donc ce n'est pas un extremum
en 3/5 positif puis négatif donc la fonction est croissante puis décroissante donc maximum local en 3/5
en 1 négatif puis positif donc la fonction est décroissante puis croissante donc minimum local en 1
Conclusion