Inscription / Connexion Nouveau Sujet
Dérivation
Bonjour à tous,
j'ai un existe qui porte sur la dérivation, je vous remercie de votre aide d'avance, voici l'énoncé :
On considère la fonction f définie par f(x)= x3-4x et dérivable sur R et la droite d d'équation y = -x+1.
Démontrer que la courbe f admet exactement 2 tangentes parallèles à la droite d en des points que l'on déterminera.
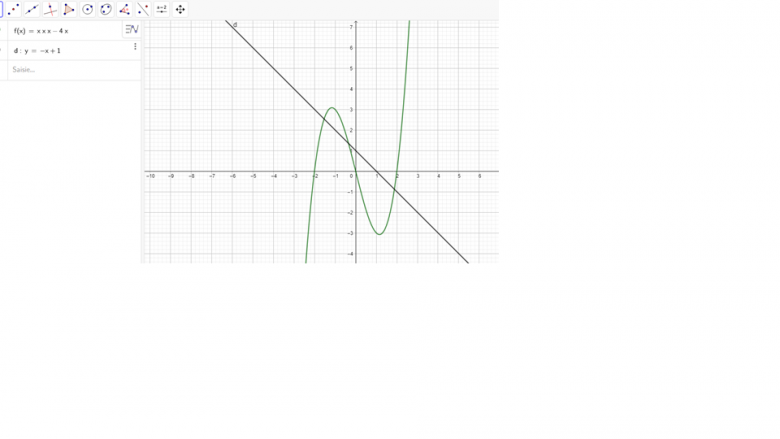
Je ne vois pas comment commencer, j'ai d'abord imaginé sous forme de graphique :
Merci
...même en dehors de ton exercice 
et quel est le coefficient directeur d'une tangente en un point d'abscisse a ?
carita
f(x) = x3-4x
f'(x)= 3x²-4
Après je dois résoudre une équation ?
3x²-4= 0
3x² = 4
x² = 4/3
x = racine de 4/3 ou -4/3. Puis je remplaces dans x dans la fonction f(x) ?
carita
J'avais eu un exercice dans le même style et je pensais que je devais faire comme ça.
J'ai la dérivé de f(x). Ensuite ?
on résout f '(x) = 0 pour trouver ses racines, par exemple pour étudier la variation de f;
mais ici ce n'est pas le cas.
on souhaite trouver la ou les valeurs de x telles que f '(x) = ...?
rappel : la ou les tangentes doivent être parallèles à la droite d'équation y = -x+1
donc...
quel est le coefficient directeur d'une droite d'équation y = mx + p ?
et donc pour la droite y = -x+1, c'est ....?
y = (-1) * x + 1 ==> le coeff. directeur de la droite (d) est donc -1.
ainsi, si l'on cherche des tangentes à Cf qui soient parallèles à (d),
on doit résoudre f '(x) = ...? (relis ton message de 15h32)
carita
Désolé pour la réponse tardive ...
Alors on a f'(x) = 3x²-4
y= -x+1 donc
f'(x) = 3x²-4
3x²-4 = -x+1
3x²-4+x-1= 0
3x²+x-3 = 0 < on reconnait le polynôme du second degré avec :
 = b²-4ac
= b²-4ac
 = 1² -4*3*-3 = 37
= 1² -4*3*-3 = 37
X1 =

 0.84
0.84
X2 =

 -1.18
-1.18
Pour trouver l'ordonné je remplacerai dans les 2 x que j'ai trouvé dans la fonction f, biensur je prendrais les valeurs excates de x.
f'(x)= -1 je dois résoudre celle-ci ?
bien sur
... désolée, à refaire - et sans discriminant

carita
Décidemment,
f'(x)=3x²-4 donc
f'(x)= -1
3x²-4 = -1
3x²= 3
x² = 3/3
x = ou -
J'aurais pu simplifier 3/3 qui donne 1
J'aurais pu simplifier 3/3 qui donne 1 ----- je ne te le fais pas dire  , et même
, et même ou -
oui c'est ça
aux points d'abscisses respectives 1 et - 1, les tangentes sont // à (d).
et tu trouves les ordonnées, comme tu as dit précédemment.
retiens bien la méthode, tu recroiseras certainement ce type d'exercice.


