Inscription / Connexion Nouveau Sujet
dérivation
Bonjour je ne parviens pas à faire cet exercice
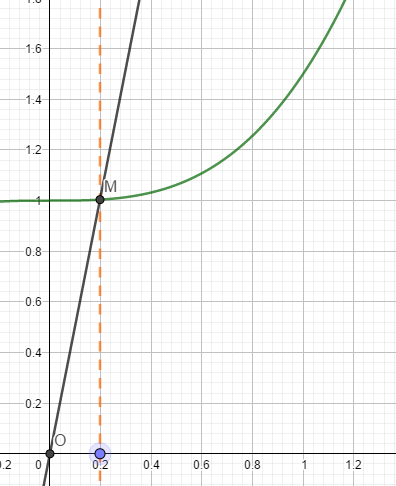
Soit f la fonction définie sur l'intervalle [0;1] par f(x)=1/2x^3+x et C sa courbe représentative dans un repère orthonormé d'origine O. A tout nombre réel h de l'intervalle [0;1], on associe le point M de C d'abscisse h.
1.a) exprimer la pente c de la sécante OM en fonction de h.
b) représenter sur le graphique les sécante pour h=1, puis h=0.5 et h=0.1
Le point M est associé à la courbe et ses coordonnés varient je ne les aient donc pas précisément pour les remplacer dans la formule
M a pour abscisse h
M est sur la courbe d'équation f(x) = 1/2 x^3 + 1
comment peux tu écrire l'ordonnée de M ?
NB : q1) on te demande d'exprimer en fonction de h.. il n'est pas question de calculer, mais d'exprimer.
l'ordonnée de M, c'est ça.
xM = h
yM = 1/2 h^3 + 1
donc tu peux exprimer la pente de OM, n'est ce pas ?
pour tracer les sécantes j'ai un problème car les ordonnées de mon graphiques s'arrêtent à 1,9
pour c(1)= 3/2 (pour celle ci c'est ok)
c(0,5)=2,125
c(0,1)=10,005
"pour tracer les sécantes j'ai un problème car les ordonnées de mon graphiques s'arrêtent à 1,9"
je ne vois pas le rapport...
explique moi comment tu fais pour placer M ..
ben non.. tu n'as pas compris ce qu'on a fait.
On a calculé le coefficient directeur de OM, pas l'ordonnée de M..
reprends ton énoncé :
M a pour abscisse h et M est sur la courbe.
h=1 : place sur la courbe le point d'abscisse 1..
oui c'est ce que je suis en train de faire mais du coup
je prend le point d'abscise 1 puis je monte a la courbe et je relis ce point, au point O(0,0) ?
Oui merci c'est ce que j'ai fait
Par contre vous avez pris une autre courbe comme exemple, car la mienne n'y ressemble pas ?
grtfi,
tu es en 1ère S : fais toi un peu plus confiance. utilise ce que tu as appris au collège et en seconde pour répondre au questions, en gardant à l'esprit le fil des questions.
OK ?
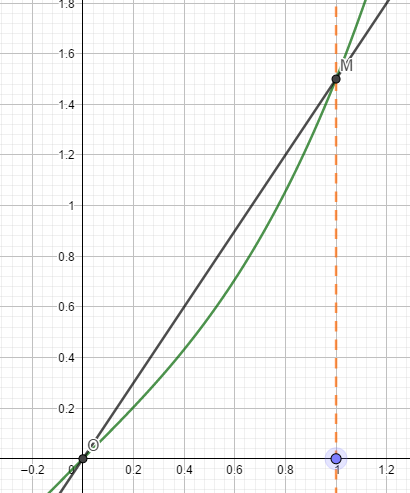
non, j'ai gardé la courbe de ton énoncé, mais sur la figure que j'ai postée, j'ai zoomé sur l'intervalle : x appartient à [0 ; 1]
je ne comprends pas pourquoi nous avons obtenus pout h=0,5 2,125 et pour h=0,1 10,005 pour ne pas s'en servir
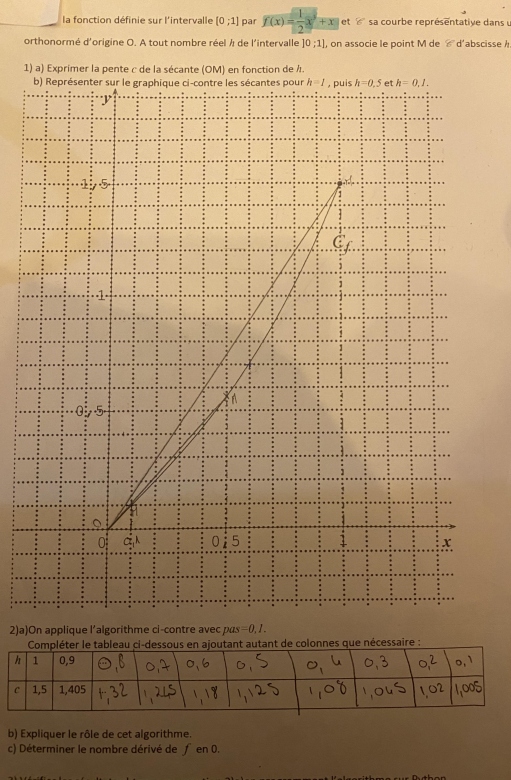
excuse moi, j'avais lu f(x) = 1/2x^3 + 1
d'ailleurs
je t'avais écrit :
M a pour abscisse h
M est sur la courbe d'équation f(x) = 1/2 x^3 + 1
et tu m'as répondu
l'ordonné de h est f(h)= 1/2 h^3 + 1 ...
tu n'as pas vu que ça ne correspondait pas à ton énoncé ?
avec f(x)= 1/2 x^3 + x
alors f(h) = 1/2 h^3 + h
et la pente de OM s'écrit (1/2 h^3 + h) / h = h(1/2 h² + 1)/h = 1/2 h² + 1
l'intervalle de ton énoncé est ]0 ; 1] avec 0 exclu, et non [0;1], comme tu l'avais écrit.
refais les calculs pour la quesion b) !