Inscription / Connexion Nouveau Sujet
derivation
Bonjour ,
J'aurai besoin d'aide pour savoir si j'ai bien compris l'exercice , je n'ai pas spécialement compris l'exercice enfin la question 1.
Pour tout réel 𝑥, on pose 𝑓(𝑥) = 𝑥3 − 3𝑥 − 1
Soit C la courbe de 𝑓 dans un repère, A le point de C d'abscisse -2 et (T) la tangente à la courbe C en A.
L'objectif est d'étudier la position relative de la courbe C et de la tangente T, c'est-à-dire : déterminer si la courbe C est au-dessus ou en dessous de la tangente T.
1. A la calculatrice, tracer la courbe C et la tangente T. Conjecturer la position relative de C et de T. Expliquer.
Dans la suite de l'exercice, on va démontrer la conjecture établie en 1.
2. Déterminer l'équation réduite de la tangente T. Justifier rigoureusement et détailler les calculs.
Pour la question 1) je n'ai pas compris comment tracé la tangente j'avais simplement compris de la tracer sur -2 mais il y a marquer que c'est le point A ( sachant mon prof m'a dit que c'était sur calculatrice donc je ne comprends encore moins )
Pour la question 2) il faudrai donc fais le calcul grâce a la question 1) : y=f'(a) x (x-a) + f(a).
je ne comprends juste pas la question une , car sur ma calculatrice je peut mettre une tangente mais je peut la mettre ou je veux...donc peut etre prendre un point au hasard ? et pour déterminer la position relative ? faire juste par rapport a la courbe et a la tangente mais ou placer la tangente ?
merci beaucoup !
bonjour,
je te joins le schéma que tu devrais voir sur ta calculatrice :
1. quelle conjecture fais tu ?
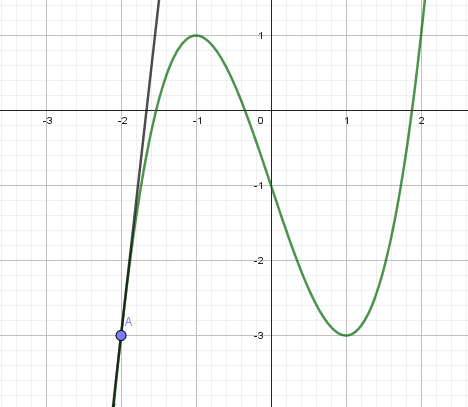
on peut supposer que quand C est au dessus des abscisse alors T est au dessus non ( alors que au debout celle-ci est ni au dessus ni en dessous car elles se croisent et sont l'une au dessus de l'autre? donc T = A aussi ? A est donc la tangente ?
A est donc la tangente ?
non, un point (A) n'est pas une tangente !
L'énoncé te dit :
A d'abscisse -2 est sur la courbe.
j'ai placé A à sa place A(-2 ; -3)
(T) la tangente à la courbe C en A.
(T) est la droite tangente à la courbe qui passe par A. : je l'ai dessinée en noir sur le schéma.
Il n'est pas question de discuter sur l'emplacement de la tangente, elle est là où je l'ai dessinée.
et au passage, ce que tu écris est incomprehensible :
"alors que au debout celle-ci est ni au dessus ni en dessous car elles se croisent" : une tangente a un point commun avec la courbe, et un seul.
donc question 1 :
là où est la tangente, à ton avis, elle est au dessus ou au dessous de la courbe ?
ok et pour justifier , je justifie juste qu'elle est au dessus de la courbe et l'intervalle ? car je n'ai pas de cours sur cette application ...
pour la question 2 j'aurai donc fais f'(a)x(x-a)+f(a)
= f'(-2) x (x-(-2)) + f(-2)
= 15 x (x+2)+13
=15x+42
y=15x+42
q1) on ne te demande pas de justifier mais d'expliquer.
Tu expliques pourquoi la tangente est placée là... (comme je te l'ai expliqué).
Q2) pour multiplier utilise * et non x (là, on ne comprend pas ce que tu écris).
j'aurai donc fais f'(a)x(x-a)+f(a)
l'équation d'une droite commence par y=
==> y = f'(a)*(x-a)+f(a)
tu as calculé f(-2) ?
et f'(x) = ??
que vaut f'(-2) ?
montre moi tes calculs, ton équation de droite est fausse.
effectivement je me suis trompé
f(-2) = (-2)3 - 3 * ( -2) -1
= -2
f'(x) = 3x2 + 3
et donc
f'(-2) = 3 * (-2)2 + 3
= 12 + 3
=15
donc y = f'(a)*(x-a)+f(a)
y= 15 * (x - (-2)) + (-2)
y = 15x + 30 -2
y=15x+29
emmma696969, sois plus rigoureuse, stp...
f(-2) n'est pas égal à -2... tu peux t'en rendre compte, puisque f(-2) c'est l'ordonnée de A...
f'(x) = 3x² + 3 est faux (erreur de signe).
recommence, vas y !
emmma696969, fais attention à ce que tu écris.
f'(x)=9 : non, c'est f'(-2) qui vaut 9
= 3x²-3 il manque le terme de gauche ! f'(x)=3x²-3
donc
f(-2) = -3
f'(-2) = 9
équation de la tangente ?
emmma696969
= 9x +15
tu ne veux pas écrire une équation correctement ?
là, ce n'est pas une équation que tu écris, il n'y a rien à gauche du signe =....
Bonjour,
Dans la suite de l'exercice, on va démontrer la conjecture établie en 1.
(Q2 équation de la tangente)
ne suffit pas, il y a d'autres questions ensuite pour démontrer la conjecture.
si tu as des problèmes pour la questions 3 et les suivantes, rappel :
toutes les questions d'un même exercice doivent être dans la même discussion, donc ici même




