Inscription / Connexion Nouveau Sujet
Dérivation
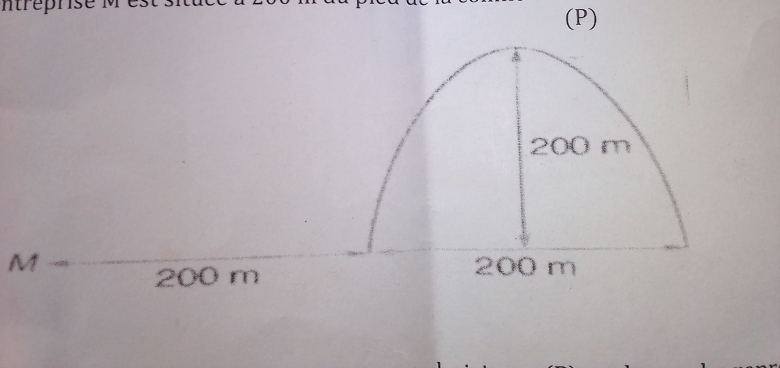
Bonsoir à tous svp j'ai des difficultés à ce devoir de maison j'ai besoin de votre aide. Une entreprise située dans la plaine à proximité d'une colline veut construire la maison du chef d'entreprise sur le sommet de cette colline. Cette entreprise désire déterminer la hauteur minimale de la maison qu'il faut afin de l'aperçoivir depuis l'entreprise. Pour cela il modélise la situation :
.la colline a un diamètre au sol de 200m et une altitude de 200m
.sa coupe par un plan vertical a la forme d'une parabole
. l'entreprise M est situé à 200m du pied de la colline
1-Démntre que dans un repère convenablement choisi que P est la courbe représentative de la fonction f définie sur [-100;100] par f(x)=10000-x²/50
2-determine une équation de la tangente à P passant par M
3-determine la hauteur minimale de la maison pour que l'entreprise puisse l'apercevoir
ah, il y avait un schéma avec l'énoncé...
montre ce que tu as fait, tes recherches, et où tu en es..
Bon j'ai considéré f(x) de la forme f(x)=ax²+bx+c avec f(100)=o
f(0)=200
f(-100)=0. Je trouve que pour f(100)=10000a+100b+c=0 ; f(-100)=-10000a-100b+c=o et f(0)=c=200 ensuite en résolvons l'équation je trouve a=-1/50 b=0 c=200 donc f(x)=10000-x²/50
tu as donc choisi un repère, tel que le sommet de la parabole soit en (0 ; 200).
ta façon de faire est bien.
Tu aurais pu aussi écrire que f(x) = a (x - 0)² + 200 = ax² + 200
et utiliser f(100)=0 pour trouver a.
Une remarque : comme tu l'as écrit sans parenthèses, tu as obtenu f(x)= -x² / 50 + 10000 je doute que ce soit ça !
mets des parenthèses !!!
f(x) = -x²/50 + 200
trouver l'équation de la tangente à la parabole passant par M
écris les coordonnées de M.
ecris la dérivée de f(x) f'(x)= ???
ensuite, il te faut trouver l'abscisse du point de tangence.
le point de tangence B a pour abscisse a et pour ordonnée ?
que peux tu écrire pour trouver cette équation ?
voyons Jauneor,
tu dis "je ne sais pas faire"... et si tu essayais de répondre à mes questions déjà ?
ecris les cordonnées de M : c'est à ta portée.
ecris la dérivée de f(x) : fais le !
quand tu postes juste "je ne sais pas faire", tu perds ton temps.
Depuis 18:00, on n'a pas avancé...
M aura pour coordonner M(x;y)
f'(x)=(10000-x²)/50
f'(x)=(-2x-(10000-x²))/50²
f'(x)=(-2x-10000+x²)/2500
"M aura pour coordonner M(x;y) " .....
J'ai l'impression que tu ne fais pas assez travailler tes méninges.
mmhh ....
M est au sol. tu ne peux pas préciser la valeur de yM ??
M est à 200m du pied de la colline... tu ne peux pas préciser xM ?
f(x) = (-1/50) x² + 200
quelle est sa dérivée ?
nb : tu as calculé la dérivée de (U(x))/(V(x)) mais 50 est une constante.. tu t'es trompé. Tu pouvais t'en rendre compte : à partir d'un polynôme du second degré ax² + bx + c , la dérivée devrait etre sous la forme 2ax+b
OK pour la dérivée.
OK aussi pour les coordonnées de M.
tu ne sais pas si c'est ça ? pour M, tu veux dire ?
tu as choisi un repère, tel que le sommet de la parabole soit en (0 ; 200). C'est bien.
l'axe des ordonnées est l'axe de symétrie de la courbe. Donc la courbe touche le sol en x=-100 et x=100 (sa largeur fait 200m).
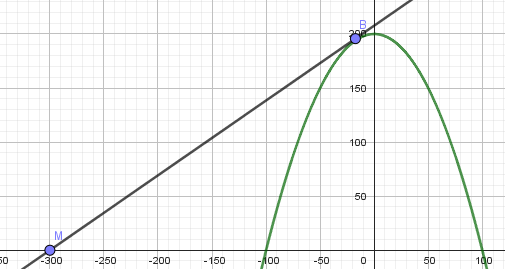
comme M est à 200m du pied de la colline, xM = -300.
Q2 : il te faut trouver l'abscisse du point de tangence.
disons que le point de tangence B a pour abscisse a
ce point B est sur la courbe : quelle est ordonnée ?
ecris f(a) = ?? et f'(a) = ??
l'équation de la tangente s'écrit comment ?
Bon je pense que si l'abscisse de B est a alors son ordonner est 0
?? tu penses que le point de tangence B a pour ordonnée 0 ?? tu crois que ce point est sur l'axe des abscisses ?
non, tu te trompes.
B est sur la courbe :
B ( a ; f(a) )
et f(a) = (-1/50) a² + 200
l'équation de cette tangente s'écrit
y = f'(a)(x-a) + f(a)
et M appartient à cette droite ==> quand x = -300, y = 0
d'où
0 = f'(a)(-300-a) + f(a)
remplace f'(a) et f(a) par leurs expressions pour avoir une équation où la seule inconnue est a : tu peux trouver a (compris entre -300 et 0). (garde les valeurs exactes).
0=f'(a)(-300+a)+f(a)
(-1/25)a(-300-a)+(-1/50)a²+200=0
12a-(1/50)a²-(1/25)a²+200=0
12a+(1/50)a²+200=0
Quand je fais le discriminant
a=-582,84 et a=-17,15
a= -17,15 est la solution à retenir, elle est comprise entre 0 et -300
donc xB = -17,15
B est sur la courbe :
yB = (-1/50)(-17,15)² + 200
yB = environ 194,18
la tangente équation sous la forme y = mx + p
a pour coefficient directeur f'(-17,15) = 0,686
et elle passe par M :
0 = 0,686 * -300 + p
p = ?
equation de la tangente ?
"Donc p=205,8 " oui
ainsi l'équation de la tangente est y=-0,686 x +205,8
ensuite tu écris "y=0" : que veux tu dire ?
question 3 : qu'en dis tu ?
Je pense que on va partir de l'équation y=0,686+205,8
y=-0,686 x +205,8 tu veux dire ? avec x !!!!
la maison est au sommet de la colline : de sa maison, il verra l'entreprise M s'il se trouve sur la droite (MB).
quelle est l'ordonnée du point d'intersection entre l'axe des ordonnées et la droite ?
autrement dit, quand x=0, que vaut y ?
sachant que la colline a une hauteur de 200m, de quelle hauteur doit etre la maison ?
Ca pas Sa !
la maison est en haut d'une colline qui fait 200m de haut et toi, tu penses que la maison doit faire 205, 8 m de haut ?
Tu vois ce que c'est une maison de plus de 200 m de haut ?
Voyons, Jauneor, c'est à la portée d'un enfant de CM2.
tu poses la maison en haut de la colline de 200m de haut, et en tout, maison + colline, ça fait 205,8 m... quelle est la hauteur de la maison ?
H=5,8 quoi ? litres ? kilos ? kilomètres ?
en effet, la maison doit etre haute au minimum de 5,80 m pour pouvoir apercevoir l'entreprise.