Inscription / Connexion Nouveau Sujet
Dérivation, aire d'un trapèze maximale
Bonjour à tous,
Je suis bloquée dans cet exercice :
On note f la fonction définie sur 
par :
f(x) = (x+3)²(3-x).
1. a) Calculez f'(x).
b) Étudiez les variations de f et dressez son tableau de variation.
c) Lorsque x décrit l'intervalle [0;3], donnez un encadrement de f(x).
2. Application
Un fabricant d'accessoires de tuning veut produire des autocollants pour le capot de certains modèles de voitures. Il souhaite que l'image, trapézoïdale, ait la plus grande surface possible.
La figure est ci joint.
Dans un repère orthonormé, P est la parabole d'équation y=(9-x²)/2.
A et B sont les points de P de coordonnées respectives (3;0) et (-3;0).
M et N sont les points de P d'abscisses respectives x et -x, avec 0
x3.
Déterminez la valeur de x pour laquelle l'aire du trapèze AMNB est maximale.
J'ai réussi la première partie de l'exercice 
, voici ce que j'ai trouvé:
1. a) f'(x)=-3x²-6x+9
b) f est décroissante sur ]-
;-3].
f est croissante sur [-3;1].
Et f est décroissante sur [1;-[.
c) 0f(x)32.
C'est pour la deuxième partie que les choses se compliquent pour moi 
Je sais que l'aire du trapèze c'est A= ( (B+b)
h )/2 , que les coordonnées de M sont (x;(9-x²)/2). Je sais un peu près la démarche à suivre, c'est à dire une étude de variation, et trouver un maximum, cependant je n'arrive pas à trouver la fonction de départ 
!
Voilà je vous ai tout dit, je vous remercie d'avance pour votre aide
bonjour
ta premiere partie est sans faute!
pour la deuxieme il faut que tu commence par calculer la surface du trapeze (tu peux calculer la moitie pour faire plus simple.
Donc en fonction de x tu calcule la position de M; et tu deduis que Strapeze = 2(xM.yM) + (3-x).yM.
Bonjour, oui A= ( (B+b)h )/2
B=la longueur AB = 6 ; b= MN = 2x et h=f(x)=(9-x²)/2 donc A(x)=(6+2x)(9-x²)/4=(3+x)(9-x²)/2=(3+x)²(3-x)/2
Comme tu dis, reste à trouver le maximum de cette fonction. il est pour x=1 en fait.
Désolé Glapion je n'avais pas vu ta réponse ! Tu as éclairé ma lanterne 
Je me penche là dessus et je vous tiens au courant ! Merci beaucoup !
J'ai juste une petite question sûrement toute bête pour toi Glapion, car je ne suis pas très bonne en calcul littéral 
quand tu fais (6+2x)(9-x²)/4 = (3+x)(9-x²)/2 pourquoi (9-x²) ne change pas ?
et (3+x)(9-x²) n'est pas égal à (3+x)²(3-x) non ?? quand j'ai développé pour vérifier je n'ai pas trouvé la même chose ..
j'ai d'abord utilisé 6+2x=2(3+x) et simplifié le 2 avec le dénominateur (et effectivement en faisant ça on ne change pas le 9-x²
puis après j'ai utilisé 9-x²=(3-x)(3+x) en remarquant que c'était un a²-b²
Bonjour, j'ai moi aussi cet exercice à faire, et je ne comprend pas :
B=la longueur AB = 6 ; b= MN = 2x et h=f(x)=(9-x²)/2 donc A(x)=(6+2x)(9-x²)/4=(3+x)(9-x²)/2=(3+x)²(3-x)/2
B pour la longueur AB = 6 je comprend, b pour MN = 2x aussi, pour la hauteur également, mais je ne comprend pas la formule. (6+2x)(9-x²)/4 ici tout est sur 4 ou juste (9-x²)?
(6+2x)(9-x²)/4 ici tout est sur 4 ou juste (9-x²)
a.(b/c)= (a.b)/c il n'y a pas de différence (=(a/c).b aussi! ; mais ne vaut pas (a/c).(b/c) attention!!!)
pour la question :
c) Lorsque x décrit l'intervalle [0;3], donnez un encadrement de f(x).
pourquoi 0≤f(x)≤32 ?
Je ne comprend pas ...
Bonjour à tous,
Je sais que ça fait un bout de temps que ce post est paru.
Mais j'ai exactement le même exercice à faire. J'ai trouvé les deux premières questions, a) et b) mais pour la c) je bloque, les autres aussi...
a) on développe l'identité remarquable cela donne (x²+6x+9)(3-x) soit f'(x)= -3x²-6x+9.
b) on a deux racines x1= -3, x2= 1.
On trouve que f est croissante sur ]-l'inf;-3] et sur [1;+l'inf[; f est croissante sur [-3;1]
c) je ne comprends pas comment on peut donner un encadrement de f(x)
Merci de votre aide
Bonjour,
en examinant ce que veut dire croissante et décroissante (tu as d'ailleurs fait une faute de frappe, j'espère que ce n'est que de frappe)
dans la partie qui nous intéresse qui est non pas R tout entier mais seulement [0; 3] : quelle sont les variations de la fonction restreinte à cet intervalle ??
alors le calcul des valeurs de la fonction au bornes de l'intervalle en son extrémum permettent de conclure.
(tous calculs faits dans la discussion au dessus d'ailleurs)
Oui ce n'est qu'une faute de frappe, je voulais dire décroissante. D'accord merci beaucoup je fais les calculs et j'enverrai un message.
Bonne soirée.
Re bonjour
c) En faisant les calculs j'obtiens une fonction f uniquement décroissante sur l intervalle [0;3] ce qui me laisse perplexe.
J'obtiens de drôles de valeurs mes extremum sont 9 et 0
ah bon ???
tu avais pourtant dit :
f est croissante sur ]-l'inf;-3] et sur [1;+l'inf[; f est croissante sur [-3;1]
en replaçant (faute de frappe) un "croissante" de ce fatras par un "décroissante", reste à savoir lequel, tu ne l'as pas dit.
cela devrait être :
f est décroissante sur ]-l'inf;-3] et sur [1;+l'inf[; f est croissante sur [-3;1]
ce qui réduit à [0; 3] donne croissante sur [0;1] (le bout de l'intervalle [-3;1]) et décroissante sur [1; 3] (le bout de [1;+l'inf[)
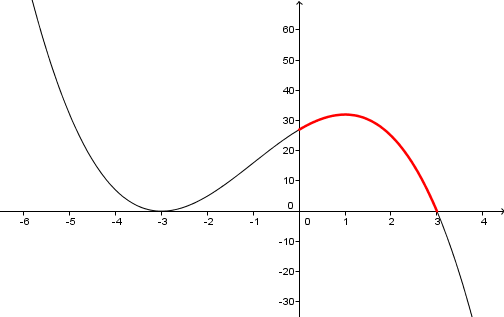
il faut calculer f(0), f(3) et f(1)
le maximum est f(1), le minimum est f(3) dans cet intervalle là
l'encadrement demandé est donc [f(3); f(1)]
encore faut il ne pas se tromper dans ces calculs arithmétiques !
(en remplaçant x par 0, 1, 3 dans f(x) = (x+3)²(3-x))
Merci beaucoup,
Je viens de finir les calculs et j'ai trouvé le bon encadrement f(x) comprise entre 0 et 32.
Je me suis rendue compte que je m'étais trompée des le départ (1er tableau de variations) ce qui a évidemment fausse mes résultats. Tout est maintenant corrigé. Jai presque terminé la deuxième partie de l'exercice avec l'aire du trapèze AMNB maximale. Je devrais trouvee normalement 1.(si je ne me suis pas encore trompée dans mes calculs)
Merci beaucoup de votre aide !
Bonne soirée
(tu as d'ailleurs fait une faute de frappe, j'espère que ce n'est que de frappe)
avec l'aire du trapèze AMNB maximale. Je devrais trouver normalement 1.
tel que tu écris ta phrase elle voudrait dire que l'aire maximale elle même est 1 ce qui est faux.
Je me suis mal exprimée
En fait l'aire sera maximale en 1, et le résultat que j'ai trouvé comme maximum en 1 est 16
Annuler
connectez vous