Inscription / Connexion Nouveau Sujet
Dérivation- Point de vue local
On considère la fonction g, définie sur [-4;3], dont on donne la représentation graphique suivante.
Seuls les points marqués d'une croix permettent une lecture graphique précise.
°T1 est la tangente à la courbe de g au point d'abscisse -2. On a tracé la droite dans sa représentation graphique.
°T2 est la tangente à la courbe de g au point d'abscisse 1. Cette tangente est parallèle à l'axe des abscisses.
°T3 est la tangente à la courbe de g au point d'abscisse -2.5 passant par les point A(2,5;-3) et B (-9,5;1).
Déterminer les équations des trois tangentes.
Je ne comprends pas comment je dois procéder pour résoudre cette exercice. Est-ce possible de me donner des pistes pour le comprendre?...
Cordialement.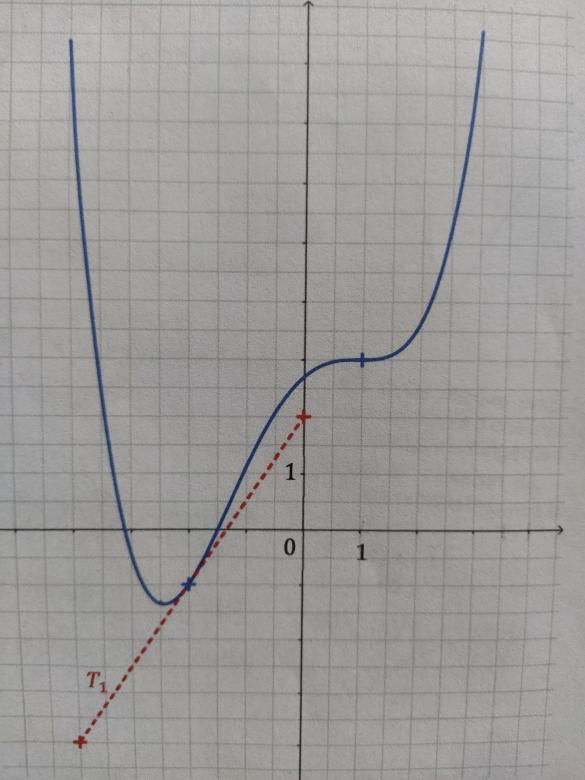
*image tournée, faire CTRL+F5*
Bonjour,
1) Tu connais les coordonnées de 2 points de la tangente T1.
Donc tu peux facilement trouver une équation de cette droite...
Bonjour
Comment écrit-on l'équation d'une droite on vous donne les 2 points
le coefficient directeur et un point
On sait qu'une équation se construit avec ax+b donc pour T1: a=- 4 et que b= 2. L'équation est donc 4x+2.
Le coefficient directeur de la droite T1 n'est certainement pas égal à 4...
Il faut le calculer !
Tu connais 2 points de cette droite.
L'équation d'une droite non parallèle à l'axe des ordonnées est de la forme ou
ax+b n'est certainement pas une équation.
Il faut donc utiliser la formule yb-ya sur xb-xa ?
C'est
Oui pour répondre à ta question 1.
Tu auras choisi au préalable 2 points de la droite T1 dont tu connais ses coordonnées.
Ok pour T1. 
L'équation de T2 est plus facile à déterminer, sa tangente est parallèle à l'axe des abscisses...
Je ne comprends pas comment déterminer l'équation de la droite, mais je sais que le coefficient directeur est égal à 0.


