Inscription / Connexion Nouveau Sujet
Dérivée
Bonjour,
J'ai besoin d'aide concernant un exercice sur la dérivation s'il vous plait .
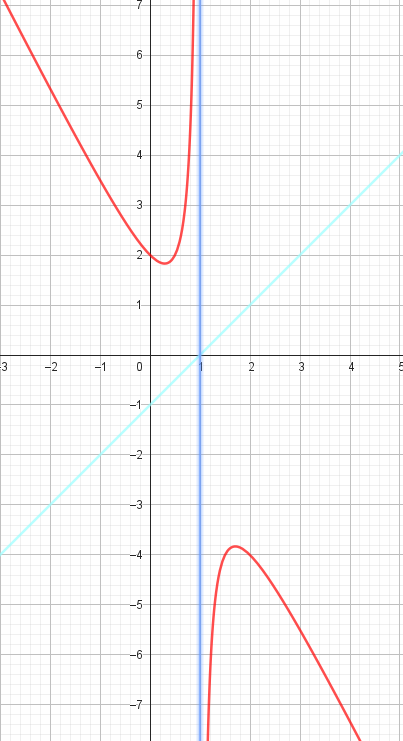
Soit f la fonction définie sur Df = \{1} par f(x)=-2x²+3x-2/x-1
\{1} par f(x)=-2x²+3x-2/x-1
On appelle Cf sa courbe représentative dans un plan apporté à un repère orthonormé.
1. Déterminer la fonction dérivée de f sur Df
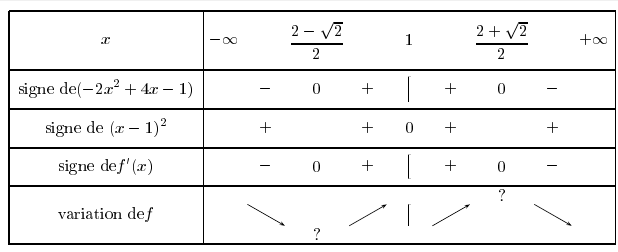
2.a. Donner le tableau de signes (x − 1)² sur Df
b. Donner le tableau de signes −2x² + 4x − 1 sur Df
c. En déduire le tableau de signe de f'(x) sur Df
d. En déduire le tableau de variation de de f(x) sur Df
3. Montrer que, pour tout x Df
Df
f(x) = −2x + 1 − 1/x-1
4. Soit d la droite d'équation y = −2x + 1
Étudier la position relative de Cf par rapport à d
5. Déterminer l'équation réduite de la tangente T à Cf au point d'abscisse 0.
6. Cf admet elle des tangentes parallèles à T ? si oui, donner l'équation réduite de chacune d'elles.
Voici ce que j'ai fait à présent :
1)f'(x)= 2*-2+3/1
f'(x)=-1/1
on note u = -2x + 3x - 2
u' = -4x + 3
on note v = x - 1
v' = 1
on sait : u'v - uv' / v²
( -4x + 3 ) * (x-1) - (-2x + 3x - 2 )* 1 / (x-1)²
f'(x) = -4x² + 6x - 1 / (x-1)² ???
Il ne faut pas confondre et
c'est-à-dire une fonction et le réel image de
par
.
il manque le carré ce qui entraîne une erreur dans le calcul de la dérivée
c'est correct mais cela ne correspond pas à la dérivée de ce que vous avez appelé u .
parenthèses indispensables (u'v-v'u)/v^2
Oui j'ai oublié d'écrire le carré : u = -2x² + 3x - 2 u'= 2*-2x+3= -4+3
f'(x)=( -4x + 3 ) * (x-1) - (-2x + 3x - 2 )* 1 / (x-1)²
f'(x) = (-4x² + 6x - 1 )/ (x-1)²
vous avez encore oublié le carré
Développez
ce que vous auriez dû écrire
u (x)= -2x² + 3x - 2 u'(x)= 2*-2x+3= -4x+3
f'(x)=(( -4x + 3 ) * (x-1) - (-2x^2 + 3x - 2 )* 1) / (x-1)²
Ah oui...
f'(x)=(( -4x + 3 ) * (x-1) - (-2x^2 + 3x - 2 )* 1) / (x-1)²
f'(x)= -4x²+4x+3x-3+2x²-3x+2/(x-1)²
f'(x)= -2x²+4x-1/(x-1)²
D'accord, d'ailleurs en lisant le texte, on trouve
2.a. Donner le tableau de signes (x − 1)² sur Df
b. Donner le tableau de signes −2x² + 4x − 1 sur Df
Ce qui permet de penser que le résultat est correct.
2.a (x − 1)² est positif
−2x² + 4x − 1 :
x | - 2-
2- 2/2 2
2/2 2  2/2 +
2/2 +
f(x)| - | + | -
Δ=b²-4ac
Δ= 4²-4*(-2)*(-1)=8
Δ>0 Cette fonction admet donc 2 solutions
x1=-4+ 8/2*(-2)= 2-
8/2*(-2)= 2- 2/2
2/2
x2=-4- 8/2*(-2)= 2+
8/2*(-2)= 2+ 2/2
2/2
Il faudrait faire un peu plus attention
Dans le tableau, vous avez oublié un signe + et la valeur exclue.
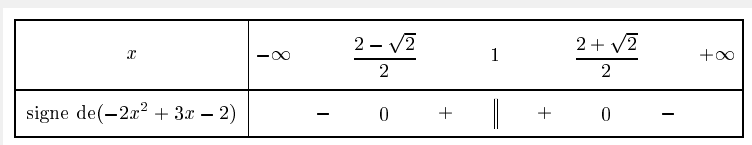
Non, il n'y a pas de changement puisque vous divisez par un réel positif
on a bien et
On pourrait dire aussi que le signe de est celui de
Dans un tableau de variation, on veut pouvoir dire quand la fonction est croissante et quand elle est décroissante.
C'est le tableau du message précédent. Je ne pense pas que vous ayez vu les limites, c'est pourquoi je n'ai rien mis. En revanche, vous avez à calculer les valeurs pour remplacer les ? .
Non, on veut tout simplement une autre écriture de
En partant de vous devez trouver
réduction au même dénominateur.
Au-dessus, en dessous
La courbe est-elle au-dessus de la droite ou en dessous, sur quel intervalle ?
Bonsoir monsieur,
S'il vous plaît personne ne donne suite à mon devoir de probabilité j'aimerais le finir mais j'ai besoin d'aide. Pouviez vous m'aider s'il vous plaît ? Merci
GeoGebra fait de très belle courbe.
À quoi sert la question 3 si ce n'est pour simplifier la réponse à la question 4
puis étudier son signe