Inscription / Connexion Nouveau Sujet
dérivée et équation réduite
Bonjour, j'ai fait un exercice d'entraînement pour un contrôle et je souhaiterais avoir une correction. Pouvez-vous m'aidez?🤗
.
.
Énoncé - Questions - Réponses
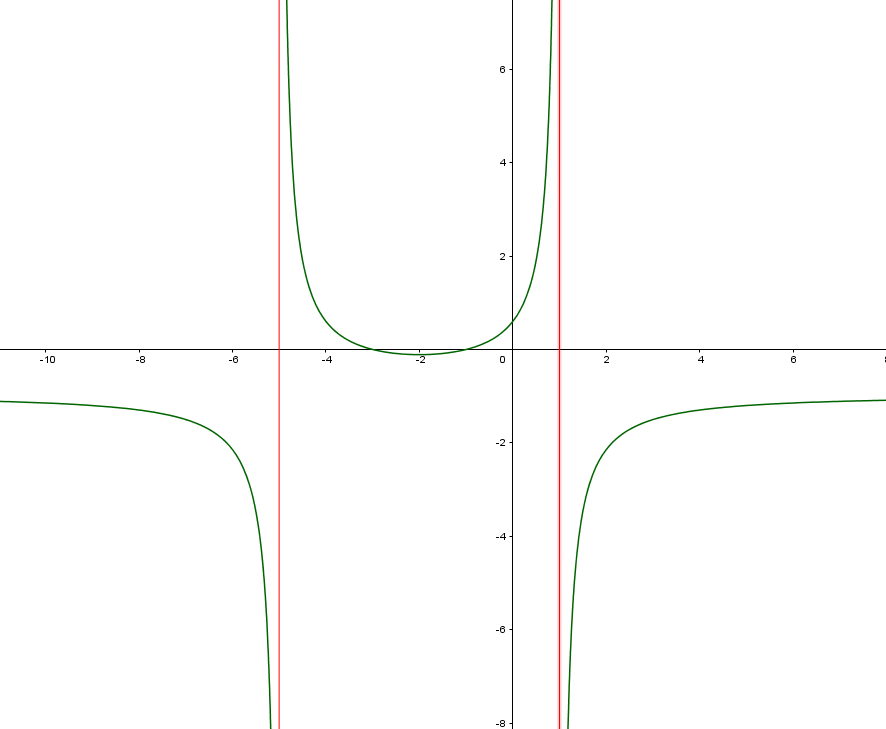
soit h définie par
1) Déterminer Dh.
--> La fonction h est un quotient, il y a donc la présence de valeurs interdites
-x2-4x+5=0 si et seulement si x=-5 ou x=1
Les valeurs interdite sont donc -5 et 1.
Ce sont des fonctions dérivables sur R donc la fonction h est dérivable sur R\ {-5;1}
2) Donner l'expression de sa dérivée et préciser ainsi le domaine de dérivabilité de h.
h(x) est un quotient donc h'(x) =
avec
résultat : Donc h'(x) est dérivable sur R\ {-5;1}
3) Dresser le tableau de variations.
À propos de 16x+32=0 si et seulement si x=-2
les valeurs interdite sont x=-5 et x=1
4) Déterminer l'équation réduite de la tangente en 3.
On sait que x=3 et que
donc et
soit y= h'(3)(x-3)+h(3)
y=
y=
.
.
Merci d'avance🤗
Bonjour
Il me semble voir des signes sur la deuxième ligne or c'est un carré donc c'est toujours positif même strictement positif puisque c'est nul pour des valeurs où la fonction n'est pas définie
Là c'est correct sauf que je n'aime pas car on étudie les variations de
donc h seulement mais les avis sont partagés (voir le professeur pour cela)
Avez-vous vu les limites ?
Avec le nouveau programme (bac 2021) nous ne calculons pas les limites, donc c'est pour ça que pour ,
, et les valeurs interdites je n'ai rien mis car ce sont des limites
C'était aussi le cas un peu avant. Elles ne se voyaient qu'en terminale en commençant par celles des suites.
Bon courage pour la rédaction, un effort sur l'orthographe.
Avez-vous vu ma remarque sur l'autre fil limites et dérivées partie 2 ?
De rien