Inscription / Connexion Nouveau Sujet
dérivée et optimisation du périmètre
Bonjour voici l'énoncé :
Soif f la fonction définie sur l'intervalle ]0, +∞[ par f(x) = x + .
1) Calculer la dérivée de f et déterminer son signe.
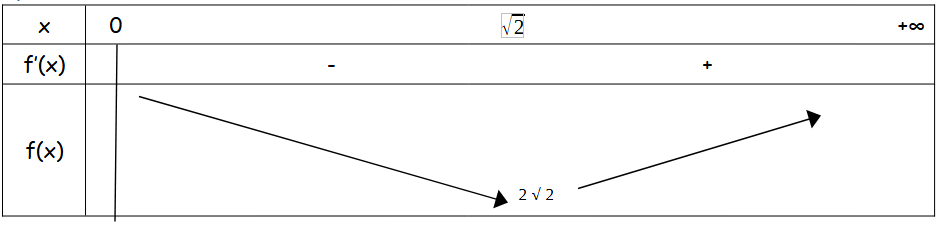
2) Dresser le tableau de variation de f
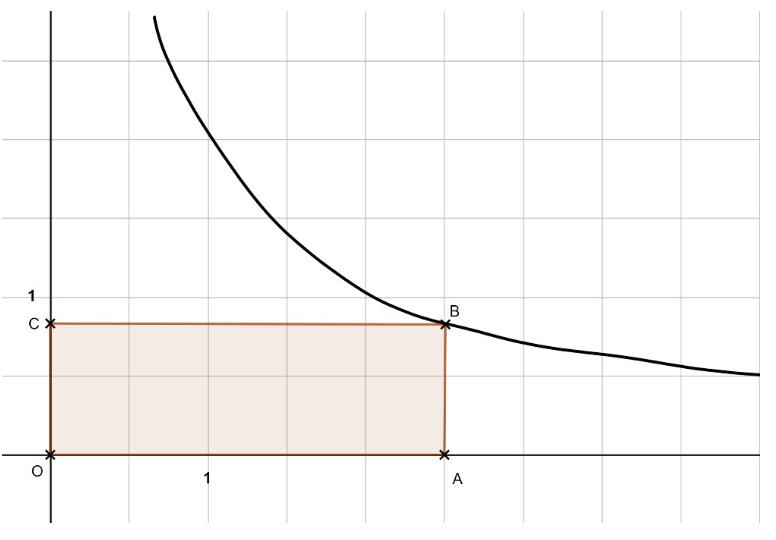
3) Le graphique ci-joint représente la courbe de la
fonction u -> : x .
Pour tout point A de l'axe des abscisses
d'abscisse a > 0 on construit le rectangle OABC.
a) Calculer le périmètre p(a) du rectangle OABC
en fonction de a.
b) Existe-t-il un rectangle de périmètre
minimal ? (*)
4) Que peut-on dire de l'aire du rectangle OABC ?
Voici ce que j'ai fait pour la question 1 :
f(x) = x +
f'(x) = 1 -
f'(x) = 0 si et seulement x² = 2
Donc f(x) est strictement positif sur l'intervalle ]-∞ ; 2[
Et f(x) est strictement négatif sur l'intervalle ]2 ; +∞[
Bonjour,
Pour justifier le signe de f'(x), résoudre f'(x) = 0 ne suffit pas.
De plus f'(2) n'est pas nul.
Réduis l'expression de f'(x) au même dénominateur puis factorise le numérateur.
N'oublie pas que tu travailles sur l'intervalle ]0, +∞[.
Je n'ai pas compris ce qu'est la fonction u du 3).
pour la question 3 je l'avais mal écrite
Le graphique ci-joint représente la courbe de la
fonction u : x ->.
Donc f(x) est strictement positif sur l'intervalle ]0 ; [
Et f(x) est strictement négatif sur l'intervalle ] ; +∞[
Heu...
On parle de la dérivée f'(x) et pas de f(x).
On a l'impression que tu joues à pile ou face.
f'(x) est du signe de x- 2.
2.
Tu as vu en seconde le signe d'expressions de la forme ax+b.
quand x < racine de 2 c'est négatif
quand x > racine de 2 c'est positif
f'(x) est strictement négatif sur l'intervalle ]0 ; [
Question n°3 :
a )
Le rectangle OABC a pour longueur a et pour largeur .
p(a) = 2*( a + )
b)
p(a) = 2f(a) = 2*( a + )
Comme f admet un minimum pour a = alors p admet un minimum aussi pour a =
.
Donc oui, il existe un périmètre minimal, atteint pour a = .
P_min = 2 ( 2 ) = 4