Inscription / Connexion Nouveau Sujet
Dérivée explication?
Bonsoir,
Quelqu'un pourrait-il m'expliquer à quoi servent les dérivées s'il vous plaît, car je ne comprends pas vraiment mis à part déterminer les variations d'une fonction...
A ce qu'il parait on peut utiliser la dérivée pour des aires, pour déterminer des vitesses, des extremums...
Eclaircissez-moi s'il vous plaît. Merci.
Bonjour ,
les dérivées sont très utiles dans de nombreux domaines scientifiques , économiques ...
C'est pour cela qu'il faut bien les maitriser à partir des cours et des exercices .
Les premières applications sont effectivement l'étude des variations des fonctions (dérivée positive fonction croissante ...)
fonction croissante ...)
Une autre application est la détermination des extremums (dérivée nulle  extremum)
extremum)
Ensuite trouver l'équation d'une courbe passant par un point et tangente à une droite donnée et un point sur cette droite .
... etc compléments ![]()
Cordialement
Merci de votre réponse.
Mais vous me dites tout ça sens vraiment m'expliquer, c'est comme-ci vous me demandiez combien de but à marquer une équipe de foot et qui sont les joueurs ayant marqué et que moi je vous répondais: 2 buts.
Sous un autre angle , les dérivées servent à mettre en équation des phénomènes physiques ou autre et ainsi de mieux les analyser .
Exemples : chute des corps , charge de condensateur , courant dans un bobinage ...
L'étude de ces phénomènes est grandement facilitée (nécessite) l'introduction de cet outil mathématique nommé dérivée
Bonjour,
A mon avis, pour mieux saisir cette notion de "dérivée" (sous entendu fonction dérivée), il est préférable au préalable de bien comprendre ce qu'est la notion de "nombre dérivé".
A ce "nombre dérivé d'une fonction en un point" correspond à ce qu'on appelle un "taux d'accroissement".
Le nombre dérivé est un cas "limite". Et c'est dans la compréhension de cette approche qu'à mon sens se situe la pleine appréhension de la notion de "dérivée" (avec un "e" à la fin).
Selon toi, que veut dire ce panneau ?

Bonsoir,
Merci de votre réponse.
Il s'agit d'une pente de 10%.
le nombre dérivé= taux d'accroissement= coefficient directeur de la tangente=pente de cette tangente ?
Mais j'ai dû mal avec la notion de fonction dérivéE comme vous dites... :/
le nombre dérivé= taux d'accroissement= coefficient directeur de la tangente=pente de cette tangente ?
Oui,c'est cela.
La fonction est dérivable en
si
existe et est finie.
Si tel est le cas, alors la fonction est dérivable en
et cette limite s'appelle nombre dérivé de
en
et se note
.
Il correspond à la pente de la tangente à la courbe de la fonction en
.
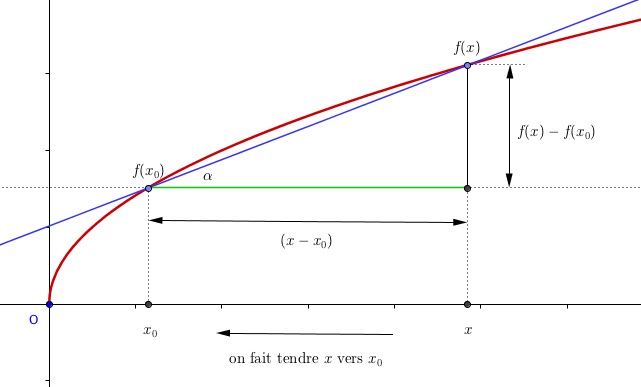
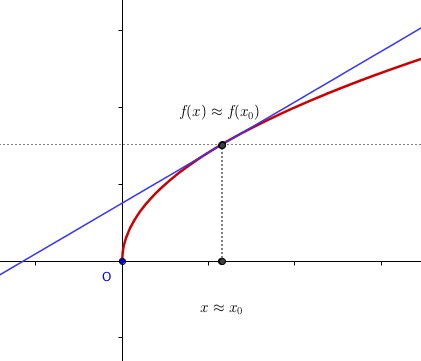
En faisant tendre vers la valeur
,
va aussi se rapprocher de
, et la droite bleue va "se tangenter" à la courbe.
Ton , c'est en fait ta valeur limite de
qui dans la première figure sera déterminer par :
c'est "la pente".
Remarque : en général, on l'apprend avec en faisant tendre y vers 0.