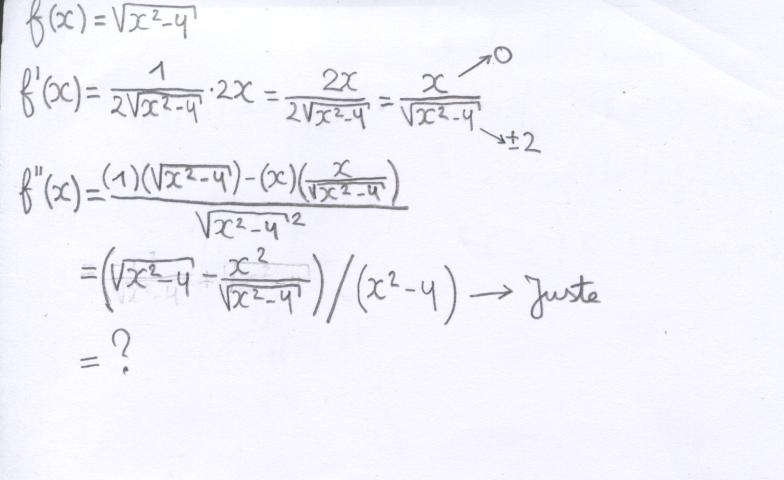
Bonjour,

comment tu as trouvé x²-4 au dénominateur alors que tu n'as pas réduit au même dénominateur dans le numérateur?

bonjour,

vérifie ton niveau et celui où tu post le message:
f(x)=

f'(x)=

simplifie déjà...
si tu es en terminale tu dois avoir une formule pour la dérivée de cette fonction donc inutile d'appliquer ma méthode.

euh, je ne vois pas trop ce que tu veux dire...
j'ai applique la formule (f/g) = (f'g-fg')/g²
le dénominateur g² c'est (sqrt(x²-4))², ce qui donne x²-4

Je ne vois pas le problème ici. En réduisant au même dénominateur ton numérateur, les x² se simplifient.

Je ne m'y retrouve pas trop dans vos explications lol
J'habite en belgique, et c'est pas le même système, c'est 6 années primaires (les petits), et 6 secondaires.
Je suis en 5eme math faible, donc j'ai pensé que c'était comme la seconde ici.

ah oui dsl, je n'ai pas remarqué ton carré au début.

Donc réduis au même dénominateur sur ton numérateur:

tu dois trouver -4/[(x²-4)rac(x²-4)]

_{Bonjour Rafalo}

merci, je vais vite essayer ça dans mon programme graphique

merci, c'est exactement ça^^
j'ai bien fait de m'inscrire sur ce forum il y a 10 min lol

pas de problème