Inscription / Connexion Nouveau Sujet
Déterminer graphiquement f'(x)
Bonjour,
j'ai quelques difficultés dans un exercices sur les fonctions dérivées.
Voici l'énoncé de l'exo :
On donne la représentation graphique de la fonction f définie sur [-3;3] par f(x)=0.5x²-1.5
a) Déterminer graphiquement f'(1), le nombre dérivée de la fonction f au point d'abscisse 1.
b) Déterminer de même f'(0) et f'(-1).
c) Sachant que la dérivée f' de la fonction f est la fonction qui a tout x de [-3;3] associe le nombre dérivé de la fonction f en x, vérifier à l'aide des valeurs précédentes que son expression est f'(x)=x
Pour la 1ere question, déterminer graphiquement ? Comment faut il faire ? Je sais déterminer avec le calcul yA-yB:xA-xB étant donné que sur le point il y la tangente donc le coefficient directeur est le nombre dérivée.
Pour la question b) Je ne sais pas comment faire. Déterminer f'(0), Ca veut dire que sur le graphique je dois faire quoi ?
Merci d'avance de votre aide.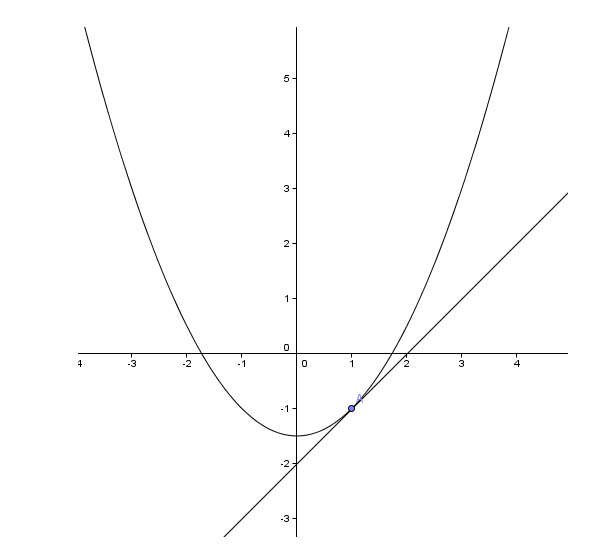
édit Océane : niveau modifié
Je pense avoir trouvé, mais je ne suis pas sur de moi.
a) le coefficient directeur est égal à la pente donc f'(1)=1
b) pour obtenir les dérivées, je trace les tangentes pour obtenir les coefficient directeur, donc
f'(0)=0 et f'(-1)=-1
c) f'(1)=1
f'(0)=0
f'(-1)=-1
Si vous pouviez me confirmer ou non mes résultats. Merci d'avance.
C'est juste Alexis93
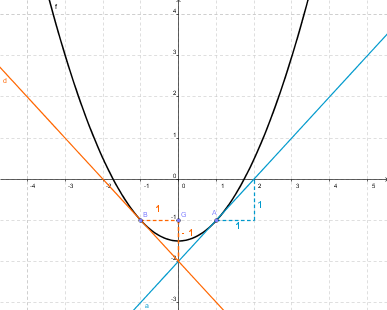
Sur le graphique , tu peux lire les valeurs en déterminant les coefficients directeurs des tangentes ( j'ai fait celles en 1 et en -1 )
J'ai un peu le même problème dans un des exercices que j'ai devant les yeux...
"La courbe C est celle d'une fonction f définie et dérivable sur R représentée dans un repère. Les tangentes à la courbe en A et B sont horizontales. La tangente en O, origine du repère, passe par le point C(-1;2).
1)Déterminer f'(-1), f'(0) et f'(2).
2)On suppose que la fonction f', dérivée de f, est définie pour tout x réel, par f(x)=-x²+bx+c.
En utilisant les résultats de la question 1, calculer a, b et c."
Je ne sais pas comment m'y prendre... 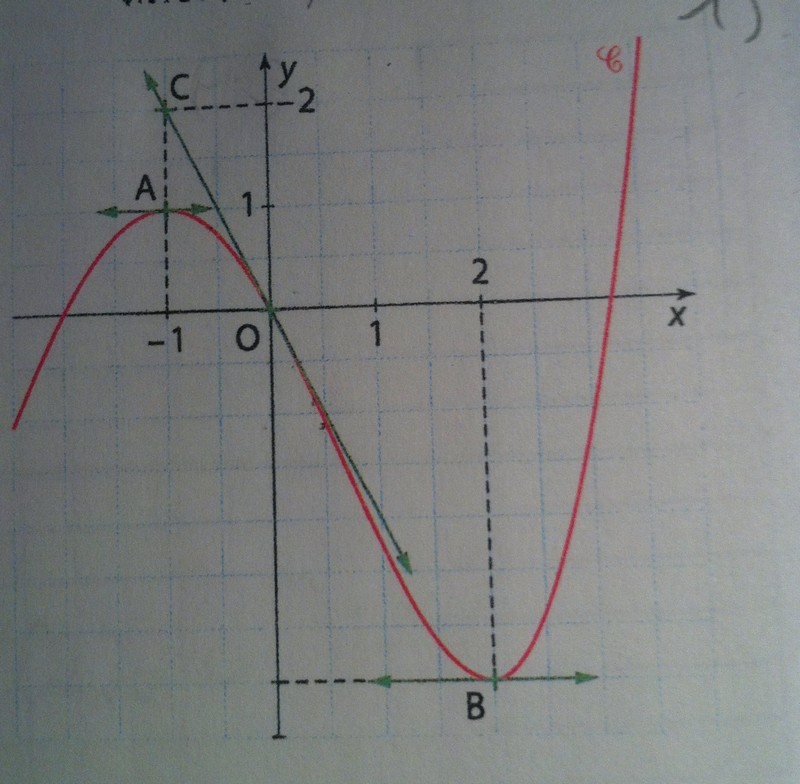
* Tom_Pascal > image placée sur le serveur de l' , merci d'en faire autant la prochaine fois Alexis93 *
, merci d'en faire autant la prochaine fois Alexis93 *
Bonsoir Cinndyd
1) f'(-1) est donné par le coefficient directeur de la tangente en -1
Cette tangente est horizontale en ce point . Quel est le coefficient directeur d'une droite horizontale ?
Donc f'(-1) = ...
Le raisonnement est le même pour f'(2) . Donc f'(2) = ...
En 0 , la tangente est une droite qui passe par C(-1;2) et par O(0;0). Te souviens-tu comment on détermine le coefficient directeur d'une droite connaissant 2 points ?
Essaie de répondre à ces questions , et on verra pour la suite .
Ah oui! Donc pour f'(-1) et f'(-2), c'est 0.
Après, je pense avoir trouvé que c'était -2 pour f'(0)...
Oui , c'est juste !
Es-tu sûre de f(x) = -x²+bx+c ? Il n'y a pas "a" et ça ne serait pas plutôt f'(x) ?



