Salut,

Déjà le x est sous la racine et donc seules certaines valeurs de x conviennent.

J'ai fais une faute lorsque j'ai recopier la fonction:
C'est Soit f(x) définit par f(x) = -x + 3 / 1+ (1 / √x)

Déterminer l'ensemble des définition Df de f(x).

La correction de l'exercice me dit :

Pour que f(x) soit calculable il faut que √x existe, donc il faut x>=0
D'autre part il faut pouvoir en calculer l'inverse ce qui impose que x soit non nul.
Donc il faut que x>0
De plus il faut  1+ (1 / √x) non nul, ce qui est toujours le cas puisque (1 / √x) >0

Conclusion Df=R*+

C'est le R avec la double barre et une petite astérisque en haut et un petit plus en bas.
Je ne comprend pas du tout.
Je me sens largué.
Peut on m'expliquer un peu la base la...

On ne demande de déterminer l'ensemble des définitions que pour les limites?

f(x) = - x + 3/1 + 1/x = - x + 3 + 1/x .
C'est ça ?

moi j'aurai tendance a mettre
Df = [0; +∞[
en réponse à la question déterminer l'ensemble des définitions de f(x).

Mais j'applique bêtement ce que je viens de lire sur un cours mais ne comprend pas le sens de cela.

non priam c'est bien
f(x) = -x + 3 / 1+ (1 / √x)
et on me demande de déterminer l'ensemble de définition en première question

Manifestement la fonction est : f(x) = -x + 3 / [1+ (1 / √x)].
Ma première réponse devrait suffire...

C'est bien ça Yzz.
Merci

Mais je ne comprend toujours pas pourquoi le bouquin me donne comme réponse:

Conclusion Df=R*+ (C'est le R avec la double barre et une petite astérisque en haut et un petit plus en bas.)

alors que moi si j'applique bêtement mais sans comprendre ce qu'est vraiment "un ensemble de définition" et si ça ne sert que aux limites
je mettrais en solution:
Df = [0; +∞[

Le petit "+" en bas signifie : "positifs" et la petite astérisque en haut signifie : "privé de 0".
Il faut bien enlever 0 de l'ensemble de déf, puisque tu as un "racine de x" en dénominateur (racine de 0 égale 0 : valeur interdite en dénominateur)

Merci beaucoup Yzz.
Mais du coup ma réponse est juste aussi?
Df = [0; +∞[

Y a t'il quelqu'un qui aurait aurait galéré sur les limites et qui aurait une réponse plus complète et surtout explicite pour quelqu'un qui n'y pige rien.

Je ne comprend toujours pas ce que veux dire "un ensemble de définition" ici. Je croyais que c'était toutes les coordonnées ou était la courbe de la fonction mais:
J'ai tracé la courbe de  f(x) = -x + 3 / [1+ (1 / √x)] et on obtient une courbe qui coupe l'axe des abscisses (environ vers x=3.5) , du coup la courbe est sous l'axe des abscisses au delà de x=3.5 et va vers +infini  de l'axe des ordonnées.
donc je ne comprend pas pourquoi cette courbe ne serait définie que sur positif....

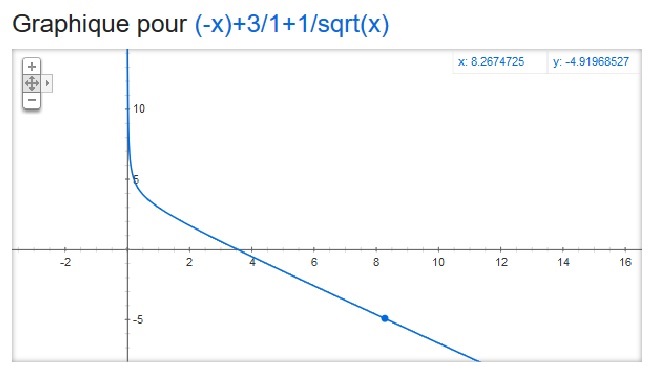
L'ensemble de définition d'une fonction, c'est l'ensemble des x pour lesquels le calcul de f(x) est possible.
Ici c'est Df = ] 0; +∞[  (0 est valeur interdite).
les valeurs de y n'ont rien à voir là-dedans.

merci.
Je crois que j'ai saisi.
demain je vous embête avec les limites a proprement parlés.

Oké