Bonjour voici l'énoncé d'un exercice sur les nombres dérivés :  
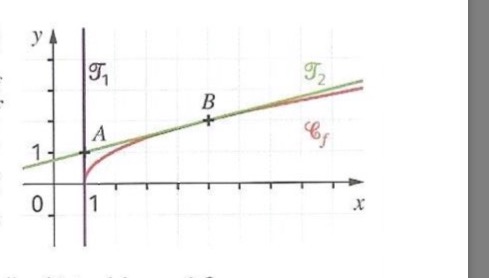
On a représenté ci-contre la courbe Cf d'une fonction f définie sur l'intervalle [1; +ainsi que 2 de ses tangentes F1 et F2

Questions:

1) La fonction f est-elle dérivable en 1 ?
2) On note b l'abscisse du point B.  Lire graphiquement la valeur de b1 de f(b) et de f'(b).

Voici le graphique :


Réponses et problèmes:
1) Ici on sait que a = 1 , donc f'(1)=? Mais comment déterminer l'équation de la fonction f ??
2) Quelle est la différence entre f(b) et f'(b) et comment les déterminer graphiquement ?
*Supposition*:
f'(b) = tangente ??
f(b)= simple droite??

Merci si quelqu'un répond précisément et aimablement à mes questions .