Inscription / Connexion Nouveau Sujet
Déterminer les dimensions du baril de volume maximum
Bonjour, pouvez vous m?aider à résoudre ce problème s?il vous plaît ? Je dois l?avoir fini pour *****mais je n?y arrive pas.
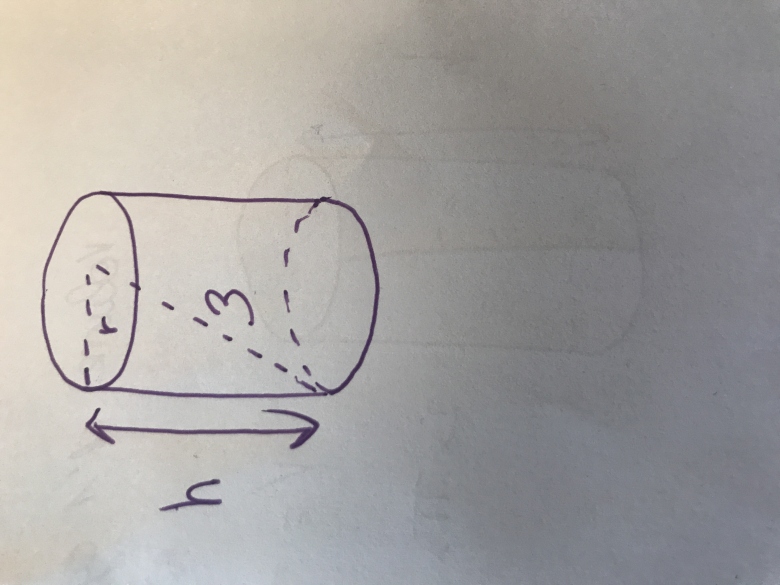
Énoncer : Pour préparer son mariage en 1612, Kepler reçu un négociant en vin. Celui-ci lui indiqua que, pour connaître le prix d?un baril, il glissait une tige en diagonale à partir du centre d?un disque De base jusqu?au fond du baril et que la longueur de tige enfoncée déterminait ensuite le prix. On s?intéresse aux barils en forme de cylindre pour lesquelles la longueur de tige enfoncée mesure 3 pieds. On note r et h le rayon et la hauteur (en pieds) du baril.
Déterminer les dimensions du baril de volume maximum.
*modération > Celilya077, pour la gestion du temps, cela dépendra essentiellement de ton investissement sur le sujet*
Bonjour
tu dis que tu dois le finir, donc tu as commencé...écris tout ce que tu as fait
![]() Sujet ancien- ne plus donner ce lien-merci
Sujet ancien- ne plus donner ce lien-merci
quelqu'un pourra alors te venir en aide
J'ai fais des recherches pour tenter de m'aider et j'avais d'ailleurs trouver presque le même sujet que moi mais je n'ai pas compris les explications.
Je me suis aidée de plusieurs recherches et j'ai fais
v(h) = pi x r^2 x h
v(h) = pi (3^2-h^2)
v(h) = 9pi x h - pi x h^3
j'ai ensuite trouver sa dérivée qui je crois est : v'(h) = 9 pi - 3pi x h^2
Après cela, j'ai fais : 9pi - pi x 3 x h^2 = 3pi (3-h^2)
= 3pi ( 3+h) (
3+h) ( 3-h)
3-h)
3pi ( 3+h) (
3+h) ( 3-h) = 0 si h= racine de 3 ou si h= - racine de 3.
3-h) = 0 si h= racine de 3 ou si h= - racine de 3.
A partir de cela je voulait faire u n tableau de variation mais je n'arrive pas avec mes résultats. J'ai donc calculer v(-racine de 3) -33; v(0) = 0; v(racine de 3)
-33; v(0) = 0; v(racine de 3) 33 et v(3)=0
33 et v(3)=0
J'en ai déduis que la hauteur maximale était d'environ 33.
J'ai effectuer ensuite : r^2 = 9-h^2 et j'ai trouver racine de 6. Ce qui correspond normalement au volume maximal.
v(h) = pi x r^2 x h
v(h) = pi (3^2-h^2) est faux, d'où ça sort ?
v(h) = 9pi x h - pi x h^3 n'est pas cohérent avec la ligne précédente
utilise * pour le signe de la multiplication
recopier sans comprendre n'apporte pas grand chose
reprends à partir de la 1re ligne et fais des choses correctes
Bonjour, j'ai le même DM à faire et je suis bloquer, je ne sais pas si mes résultats sont bon d'après ce que j'ai vue ici.
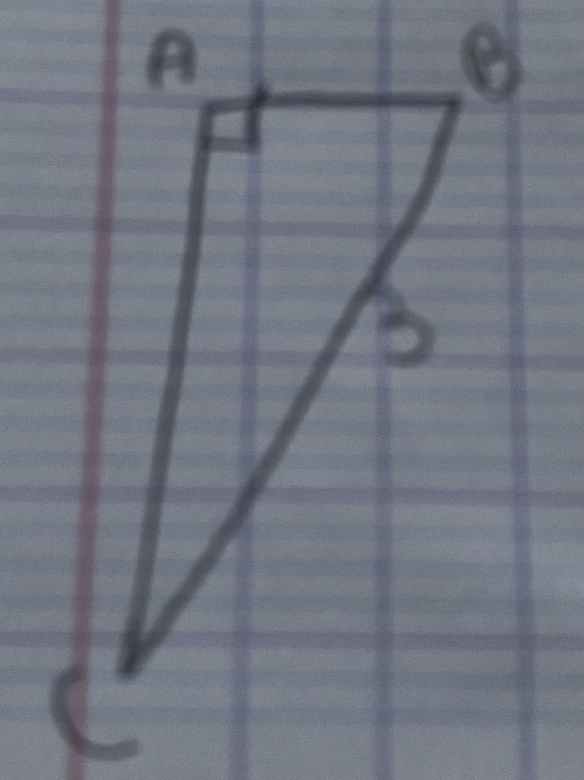
J'ai d'abord commencer par cherche le côté adjacent et opposé avec la trigonométrie. Mais étant donné qu'il n'y a pas les ° du triangle dans l'énoncé je doute de mes réponses.
bonjour,
la trigo ? s'il n'y a pas de valeur d'angle, ça n'est pas une bonne piste..
qu'avais tu trouvé ??
exprime le volume d'un cylindre avec h et r :
vas y !
J'ai noter la formule du volume oui
V=pi*r2*h
Mais ducoup je n'est pas réussi à trouver les valeurs de r et h ou bien dérivé la formule. et pour la trouver les valeurs des angles j'ai soustrait 90 ce qui donne 45 et donc j'ai fait cos et sin 45
laisse tomber la trigo : tu inventes là....
V = pi * r² * h on est d'accord.
à présent, regarde le triangle formé par la tige, le rayon et la hauteur.
Il est rectangle : applique pythagore,
vas y !
si tu ne me montres pas ce que tu écris, et que tu dis juste "je suis bloquée", je ne peux pas t'aider.
montre comment tu appliques pythagore dans ce triangle.
en effet,
si r² = 6, alors r= 6
6
ça, c'est pour le baril de droite (r > h)
pour le baril de gauche, on dira r= 3 et h=
3 et h= 6 (là, r < h)
6 (là, r < h)
tu as tout compris ? (je me demande si tu as tout suivi ....).


 (9-h^2)h
(9-h^2)h