Inscription / Connexion Nouveau Sujet
déterminer les éléments de symétrie d'une courbe
Bonjour,
Je un exercice de Maths que je ne comprends pas trop...
Voici l'enoncé :
On dit que D est centré en α si et seulement si:pour tout h∈ ℝ:
[Si α+h ∈ D alors α−h∈ D]
On considère une fonction f définie sur son domaine de définition
Df centré en α et Cf la courbe représentative de f dans le repère orthogonal (O;⃗i;⃗j).
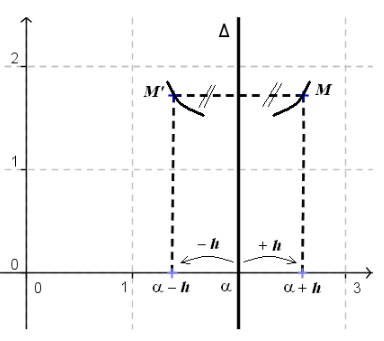
La courbe Cf admet un axe de symétrie ∆ d'équationx=α si et seulement si : pour touth∈ℝ: f(α+h)=f(α−h)
En appliquant cette méthode à la fonction
f: la fonction f définie sur Df=ℝ∖{2}par: f(x)=(x−1)(x−3)/(x−2)2
montrer que Cf admet un axe de symétrie
Quelqu'un pourrait m'aider ou expliquer comment faire,
je sais qu'il faut appliquer la formule f(α+h)=f(α−h) avec la fonction f mais je sais pas comment,enfin quelles donner faut mettre pour alpha , h ? ...
je sais qu'il faut appliquer la formule f(α+h)=f(α−h) avec la fonction f mais je sais pas comment,enfin quelles donner faut mettre pour alpha , h ?
tu laisses α et h. Ensuite tu te diras que l'égalité doit être vérifiée pour toutes valeur de h et tu pourras sûrement en déduire la valeur de α .
Bonjour,
Ecris que f(
+h) = f(-h) pour la forme particulière de f que l'on te donne, et essaye de trouver une valeur de telle que les termes en h disparaissent.
Un œil exercé pressentira que la bonne valeur est = 2, car on a un terme en (x-2) et deux termes (x-1) et (x-3) symétriques autour de 2.
Maintenant, il faut le démontrer rigoureusement...
Bonjour
un axe de symétrie ∆ d'équation
: pour tout h∈ℝ:
à montrer
Bonjour,
Je pas trop compris ce que vous voulez dire par " tu laisses α et h" ,
h est une inconnue qu'il faut que l'on determine aussi ?
Bonjour,
' vous pouvez donc donner la valeur de \alpha "
sur le graphique, alpha est egale a 2.
" donc h est un réel quelconque il va falloir travailler avec "
Faut donc remplacer x dans la fonction par h si je comprend bien ?
" à montrer"
comment je pourrais montrer ca? , je pas trop compris comment ? vous pouvez m'expliquer davantage svp ?
Tu écris :
(+h-1)(+h-3)/(+h-2)² = (-h-1)(-h-3)/(-h-2)²
Et tu essayes de trouver une valeur de telle que l'équation soit vérifiée pour toutes les valeurs de h.
oui c'est la seule valeur pour laquelle la fonction n'est pas définie
si vous supposez que c'est une autre valeur alors il existera une valeur pour laquelle
est définie mais pas
il faut calculer et montrer que c'est égal à
hekla
je fais :
f(2+h) = (2+h-1) (2+h-3) / (2+h-2)2
je developper :
4 + 2h - 6 + 2h + h2 - 3h -2 -h +3 / 4+h2 + 4
sauf que je me retrouve avec
f(2+h) = -1 + h2 / 4+h2 + 4
et la je bloque ...
LeHibou
je fais le calcul sur (α+h-1)(α+h-3)/(α+h-2)²
je developper : 2α + αh - 3α +hα -3h - α -h +3 / α2 +h2 - 4
du coup en diminuant je trouve ( en reduisant ) :
-2α + 2αh - 4h + 3
-----------------------
α2+h2-4
mais ici je bloque et je pense meme avoir fait une erreur ...
Pourquoi faire simple quand on peut faire compliqué !
il faudrait revoir les tables d'addition
je comprend pas trop pourquoi vous avez ecrit f(2+h) = (h+1) (h-1 ) / h2
?
moi j'avais remplacer dans l'expression de la fonction f
Du coup je developper
et je obtenu = h2-h+h-1 / h2 = -1
mais je pas obtenu par simplification le -h qui est dans la formule,
je trouver que -1
f(2+h) = - 1
?
d'abord il faudrait mettre des parenthèses
vous devez savoir que identité remarquable
on a donc
revoir les fractions
par conséquent si l'on change en
le résultat est le même
d'abord il faudrait mettre des parenthèses
vous devez savoir que
on a donc
revoir les fractions
par conséquent si l'on change
du coup pour la reponse de l'exercice (montrer que Cf admet un axe de symétrie ) ,
j'ecris apres avoir effectuer tous les calculs que Cf admet un axe de symétrie ∆ d'équation x=2 si et seulement si : pour tout h∈ℝ: f(2+h)=f(2−h) ?
salut
la forme canonique de (x - 1)(x - 3) donne immédiatement la réponse ...
? j'aimerais bien savoir comment ?
j'écrirais d'abord la définition
admet la droite
d'équation
comme axe de symétrie si et seulement si
pour tout tel que
et
les calculs
la conclusion
je n'écris jamais de définition ... en introduction ...
je conclus en évoquant la définition ...
mais le travail d'introduction est bien sur l'utilisation de cette définition !!!
je ne dis jamais ce que je vais faire, je le fais ... et je conclus pour répondre à la question ...
le lecteur (quand il est prof sait évidement de quoi je parle donc pourquoi je fais ce que je fais) n'est là alors que pour contrôler que je fais bien ce qu'il faut faire ou pour me corriger ou me guider si je fais fausse route ...
je vous remercie a tous les deux et aussi aux autres pour l'aide accorder.
Je pense que maintenant je compris mieux l'exercice et ce qui est demander.
je n'écris jamais de définition ... en introduction ...
je conclus en évoquant la définition ...
mais le travail d'introduction est bien sur l'utilisation de cette définition !!!
je voulais dire que pour repondre au probleme poser d'evoquer la relation qu'on nous donne en haut et effectuer les calculs et conclure sur la reponse qui semble evidente,
car on nous dit MONTRER donc cela veut dire qu'il y a bien un axe de symetrie.
Annuler
connectez vous