oups je me suis trompée de forum ...

Désolée c'était pour des dévirée et non limite

Pourquoi "trompée de forum " ?

re bonjour Karine,

alors, ce que je t'avais envoyé l'autre jour

Merci malou

j'ai de la difficulté a comprendre la citation.

Par exemple j'ai Y'' s'annule en x=-3 et x=0

max en a pour f'(a) = 0 et f"(a)< 0 (car donne concavité vers le bas)
et
min en a pour f'(a) = 0 et f"(a) > 0 (car concavité vers le haut)

donc si je dis x=-3
f'(-3) = -108 + 162
f'(-3) = 54 donc c'est pas un min ni un max ? mais seulement un point d'inflexion?

Si je dis x=0
f'(0) = 0
f''(0) = 0 encore ... ce n'est donc ni un min ni un max car f'' s'annule aussi?

je n'ai donc ni maxima ni minima mais seulement 2 points d'inflexions?

attends...

tu passes trop vite "au dessus" de ce que te fournit ta dérivée première comme indications

y'= 4x³+18x²=2x²(2x+9)

ta dérivée première s'annule pour x²=0 ou x=-9/2

soit pour
x=0 ou x=-9/2

pour 0
la dérivée seconde vaut effectivement 0, (ce n'est ni un max, ni un min,) c'est un point d"inflexion

pour x=-9/2
tu calcules f"(-9/2) et tu vas savoir si c'est un min ou un max

OK ?

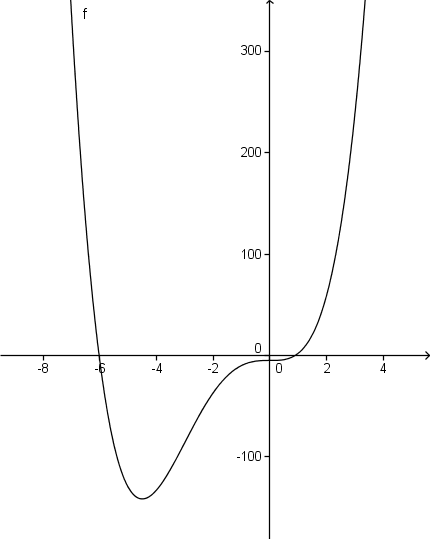
et sur la courbe, tu vois qu'en 0, tu as un point d'inflexuion
et qu'en -9/2, tu as un mini

et qu'il n'y a rien d'autre à voir en tant que min, max ou point d'inflexion...

OK ?

ha ok je fais un test sur la première dérivée ... humm je comprend ton explication.

j'ai donc

y'= 4x³+18x²
y''= 12x²+ 36x

max en a pour f'(a) = 0 et f"(a)< 0 (car donne concavité vers le bas)
et
min en a pour f'(a) = 0 et f"(a) > 0 (car concavité vers le haut)

f''(-9/2) = 12(81/4) - 162
f''(-9/2) = 243
donc x=-9/2 serait un minimum

f''(0) = 0 + 0 donc 0 c'est un point d"inflexion en suivant les règles que tu m'a inscris.

Par contre lorsque je fais le teste de la dérivée seconde que sa s'annule en x=-3 ce qui n'est pas le cas pour la dérivée première.
Le point x=-3 serait t'il aussi un point d'inflexion ou un maximum ? est-ce que je peux faire un test qui me permettre de savoir ce qui caractérise ce point?

Merci encore pour ton aide

alors, une fois que tu as tiré toutes les informations possibles grâce à ta dérivée première, tu peux terminer de travailler avec la dérivée seconde

point d'inflexion : dérivée seconde qui s'annule en changeant de signe

y"=12x²+36x
y"=12x(x+3)
s'annule en 0 et en -3

signe
-3 0
- 0 + 0 -

donc tu as une dérivée seconde qui s'(annule 2 fois en changeant de signes, donc tu as bien 2 points d'inflexion

voilà !

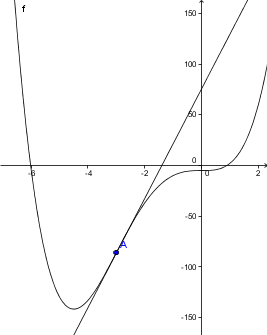
j'ai mis le point A d'abscisse 3
et j'y ai tracé la tangente
voilà ce que ça donne

point d'inflexion : tu as une courbe qui "traverse" sa tangente (puisque au niveau du point de tangence, tu as un changement de concavité)

Haha c'est ce calcul que tu avais fait la dernière fois que je comprenais pas trop.

Pour trouver mon tableau des signes comem tu as fait plus bas, je dois dire f(-4), f(-1) etc.. oubien f''(-4), f''(-1)?

signe
   -3    0
-  0  +  0  -

ouff c'est mélangeant tout ça pour ma petite tête.

alors, en France, dans les programmes, on apprend ça aux élèves
un polynôme du second degré (12x²+36x) est du signe du coefficient de x² à l'extérieur des solutions si elles existent

ici, ses solutions sont -3 et 0
le coeff de x² est 12 qui est > 0

donc je positionne mes deux solutions, -3 et 0
et je mets des + à l'extérieur et un moins entre les solutions
d'où le signe sans faire d'étude particulière

ça va ?

Désolée

"et je mets des + à l'extérieur et un moins entre les solutions
d'où le signe sans faire d'étude particulière"

je comprends pas pourquoi tu mets des + a l'extérieur et un - au centre et encore moins pourquoi ça donne l'inverse au final :

signe
   -3    0
-  0  +  0  -


J'ai jamais compris d'ou venait cela et pourtant cela semble si évident pour vous haha

mea culpa...je me suis trompée en écrivant les signes;...ça n'aide pas...!....

-3 0
+ 0 - 0 +

je vais t'envoyer un exemple détaillé après...

exemple
2(x-1)(X+3)

si tu développes
2x²+4x-6

donc polynôme du second degré qui s'annule pour -3 et 1

pour connaitre le signe, il faudrait faire un tableau de signe

x -3 1
signe de 2
signe de (x-1)
signe de (x+3)
signe du produit

et en faisant ça complètement, tu remarques que à la dernière ligne, tu as toujours le signe de 2 (ici +) à l'extérieur des solutions, et signe contraire entre les solutions

et bien sûr cela se démontre dans le cas général

car si ton polynôme s'annule pour deux valeurs x' et x"
cela veut dire qu'on peut le factoriser en a(x-x')(x-x") avec a coeff de x²

et à la dernière ligne du tableau, on retrouve le signe de "a" à l'extérieur des solutions
voilà d'où cela vient!