Bonjour,
Sujet ancien- ne plus donner ce lien-merci
pas d'énoncé pas d'aide

corriger ça en réponse ici même
satisfaire aux règles dès le départ fait gagner du temps, surtout à toi.

bonjour, j'aurai vraiment besoin d'aide ******j'ai un dm a rendre pour ******mais je ne comprend pas voici mon énoncé :
sur la figure ci-contre, MNPQ est un rectangle inscrit dans le demi-cercle de centre O et de rayon OI=5.
On se propose de determiner la position de point M sur le segment [oi] telle que l'aire du rectangle MNPQ soit maximale.

1. On note et l'aire du rectangle MNPQ.
a) Demontrer que .
b) Pour tous nombre reel de [0;5], on pose .
justifier que les fonctions A et B ont le meme sens de variation

2.a) Determiner la fonction derivee de la fonction B
b) Terminer l'etude

Merci d'avance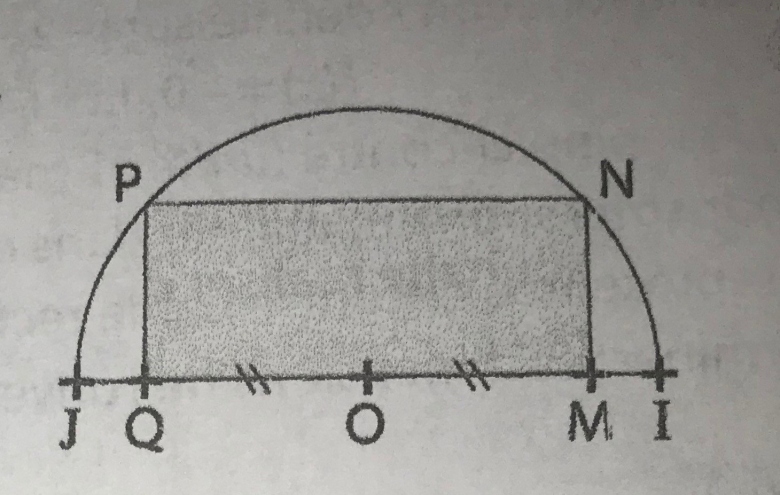



*** message déplacé ***

Bonjour, pour calculer l'aire du rectangle en fonction de x, tu as déjà QM (qui vaut deux OM), il te reste à trouver MN. Pense à Pythagore dans le triangle OMN.

*** message déplacé ***

et heureusement qu'on avait dit en réponse et dans la même discussion .... tu fais tout ce qu'il ne faut pas faire pour avoir des réponses rapides...

1a : dans le triangle rectangle OMN, Pythagore permet de calculer MN (en littéral, en fonction de x) et donc finalement l'aire du rectangle en fonction de x

etc.

*** message déplacé ***

tu sais lire ?

Glapion Je ne comprend pas comment utiliser pythagore sachant que je connais que la longueur OM

malou oui mais je connais pas trop le site

décidément tu ne sais pas lire
lis ton énoncé ! tu as une autre indication !

malouOui mais si je suis sur ce forum c'est que je ne comprend pas mon exercice
normalement vous êtes sur ce forum pour aider les gens pas pour les décourager en les rabaissants

un point sur un cercle est à quelle distance du centre ?

un point sur un cercle est à quelle distance du centre ?

mathafou5cm?

je ne rabaisse personne
pour que les aides trouvées sur des forum soient efficaces, l'élève doit réellement s'investir, sinon, cela ne servira à rien
j'indique seulement que savoir lire est indispensable
on te donne le rayon de ton cercle que je sache dans ton énoncé

quand mon Internet rame ça bégaie.

mathafou c'est pas grave

je te passe la main mathafou

oui, ON = ?
comme dit malou faut un peu se prendre en main et se réveiller, là ...
(sinon ce ne sera pas fini demain )
donc tu écris directement Pythagore maintenant que tu as tout, et tu peux même terminer la question 1 dans le même message et pas au compte goutte.

mathafouj'ai trouvé





et apres je suis bloqué

comment calcule-t-on l'aire d'un rectangle ?

malou

ducoup


par contre je sais pas comment calculer ça

il faut éviter de mettre du texte dans les formules Latex, ça fait un peu moche
ou alors ilfaut le faire exres et memtre les bos mots clé LaTeX
quand on a des "décorations" : symboles spéciaux, mise en exposant, LaTeX etc il est fortement recommandé (voire obligatoire d'utiliser le bouton Aperçu avant de poster

donc la question est terminée.

question 1b : quel est le sens de variation de la fonction carré pour X > 0 (rappelons que 0 ≤ x &le 5, que une aire c'est quelque chose de positif)

question 2a ensuite (rien à voir avec la question 1b, ce sera pour la 2a ce calcul) pour le calcul, le carré d'un produit c'est le produit des carrés
et le carré d'une racine c'est ce qui est sous le radical si ça existe (si c'est ≥0)
devrait être instantané en première.

oui j'ai pas fait exprès d'écrire en LaTex
donc si j'ai bien compris
1.b)


Donc est croissante et est également croissante

2.a)

et pour la 2.b) que veux dire terminer l'étude

et le 2x devant la racine, où est-il passé ?

ah oui pardon


et

bouh lala....opérations de calculs élémentaires
reprends

ah non mince

messages croisés
B(x) est complètement faux

ah

c'est ou que ca ne vas pas

relis 25-04-19 à 17:22 de mathafou

la 1b n'a rien à voir avec ce que tu calcules
en plus tu ne démontres rien du tout car tu ne fais que affirmer sans aucune justification

je répète : le développement de B(x) c'est pour la 2a
la 1b est une question absolument d'ordre général qui se traduirait ainsi :

quelle que soit la fonction A(x) du moment qu'elle est >0
justifier que la fonction B(x) = (A(x))² a les mêmes variations que A(x)

les expressions de A(x) et encore moins de B(x) n'ont absolument rien à faire dans cette question, à part pour vérifier l'hypothèse A(x) > 0 nécessaire à la justification.

oui mais pour montrer que B(x)=(A(x))² il faut bien trouver B(x) non?

y a quelqu'un?

non absolument pas
parce que ça c'est vrai quelle que soit la fonction A(x) (moyennant des conditions)
que ce soit celle de l'énoncé ou une autre

et la clé est
quelles sont les variations de la fonction z --->z² quand z >0 ?
(de la fonction carré) et j'ai écrit exprès z parce que ce n'est pas le carré de x du tout, c'est le carré de la fonction A(x)
il s'agit donc d'étudier les variations d'une fonction de fonction, d'une fonction composée
de x --> z = A(x)
suivie de z --> z²
donc au final de x --> (A(x))²
la propriété générale est que si g : z --> g(z) est croissante
alors g(f(x)) a les mêmes variations que f(x) (avec les intervalles de définitions qui vont bien)
et si g est décroissante alors g(f(x)) a les variations inverses de celles de f(x)

ici f(x) c'est A(x)
et g(z) c'est z²

c'est CELA la question 1b.