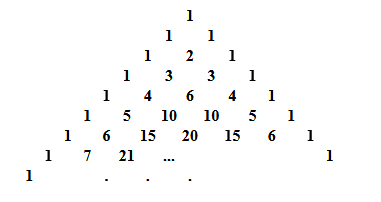Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première Probabilités et dénombrementTopics traitant de Probabilités et dénombrement [tout]Lister tous les topics de mathématiques

1 2 3 +

Niveau première
Partager :

Développement : binôme de Newton .

Posté par
Othnielnzue23 11-01-20 à 11:05

Bonjour à tous .

Merci d'avance .

1) Développer les expressions suivantes : (x+1)5  ; (x-2)6  ;  (3x+2)4.

2)

a) Développer (x+1)n

b)En déduire le nombre de sous ensemble à n éléments .







Mes réponses .

1) On sait que (a+b)ⁿ=C0naⁿ+ C¹n an-1b+....+Cn-1n+Cⁿnbⁿ.

Alors (x+1)5=x5+5x⁴+5x15
=
x5+5x4+5x+1

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 11:16

Bonjour

incomplet  Il y a des termes en x^2 et en x^3

Développez à partir de  (x+1)^2(x+1)^3 ou \left((x+1)^2\right)^2(x+1)

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 11:40

Bonjour , merci .

(x+1)5=(x+1)³(x+1)²=(x³+3x²+9x+1)(x²+2x+2)

=x5+2x⁴+2x³+3x⁴+6x³+6x²+9x³+18x+x²+2x+2

=x5+5x⁴+17x³+25x²+20x+2

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 11:47

hekla @ 11-01-2020 à 11:16

Bonjour

incomplet  Il y a des termes en x^2 et en x^3

Développez à partir de  (x+1)^2(x+1)^3 ou \left((x+1)^2\right)^2(x+1)
et si on demandait d'utiliser la formule du binôme de Newton ?

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 11:48

Non  

erreurs dans l'identité (x+1)^2.\quad  (x+1)^2=x^2+2x+\red{1}

et (a+b)^3=a^3+3a^2b+3ab^2+b^3  donc (x+1)^3=x^3+3x^2+3x+1

les coefficients binomiaux sont : 1 5 10 10 5 1

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 11:54

(a+b)^n=C_n^0a^n+C_n^1a^{n-1}b+\dots+ C_n^{n-2}a^2b^{n-2}+ C_n^{n-1}ab^{n-1}    + C_n^nb^n

Appliquez-la alors.

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 12:03

Triangle de Pascal

Développement : binôme de Newton .

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 12:13

Merci .

On obtient donc : x^{5}+5x^4+10x³+10x²+1

Si on applique le binôme de Newton:

1x^5+5×x^41x^5+5×x^4×1+ je suis un peu bloqué , comment calculer Cn-2n ?

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 12:28

(x+1)^5 =C_5^0\,x^5+C_5^1\,x^4+C_5^2\,x^3+C_5^4\,x+C_5^5\,x^0

(x+1)^5=x^5+5x^4+10x^3+10x^2+5x+1

Le n ici est connu  il vaut 5 donc n-2 vaut 3

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 12:39

Ok merci beaucoup .

Comment calculer les combinaisons avec sa calculatrice ?

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 13:01

Quelle calculatrice ?

TI  n math prob 3 p pour C_n^p

Casio menu  run exe    OPTN   -> (F6) Prob (F3) n C r (F3)

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 13:20

Donc (x-2)^6=C_6^0\,x^6+C_6^1\,x^5+C_6^2\,x^4+C_6^5\,x^3+C_6^4\,x^2+C_6^5\,x^1+C_6^6\,x^0

=x^6+6x^5+15x^4+20x^3+15x^2+6x+1

(3x+2)^4=C_0^4\,x^4+C_1^4\,x^3+C_2^4\,x^2+C_3^4\,x+C_4^4\,x^0

=x^4+4x^3+6x^2+4x+1

2) a-

(x+1)^n=C_0^n\,x^n+C_1^n\,x^n-1....+C_3^n\,x^n-3...


Comment calculer C_2^n ?

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 13:23

Oups 2) je reversé les choses , veuillez m'excuser et lire au bon sens c'est à dire : C_2^n

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 13:24

Reoups C_n^2

Posté par
Pirhore : Développement : binôme de Newton . 11-01-20 à 13:45

Bonjour,

en attendant le retour d'hekla que je salue

\large C_n^2=\dfrac{.....}{....}

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 13:56


\large C_n^2=\dfrac{A_n^2}{2!}=\dfrac{n×(n-1)}{2×1}=\dfrac{n²-n}{2}

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 13:58

1^n=1\qquad 1\times a=a donc le premier développement  était simplifié

Je vous ai écrit le développement  de (a+b)^n

par conséquent  il fallait donc l'appliquer

(x-2)^6=C_6^0\times x^6\times (-2)^0+C_6^1\times  x^5\times (-2)^1+C_6^2\times x^4\times (-2)^2+C_6^3\times x^3\times (-2)^3+C_6^4\times x^2\times (-2)^4+C_6^5\times x^1\times (-2)^5+C_6^6\times x^0\times (-2)^6

Bonjour Pirho

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 14:42

Ok merci .

Donc (x-2)^6=C_6^0x^6(-2)^0+C_6^1x^5(-2)^1+C_6^2x^4(-2)²+C_6^3x^3(-2)^3+C_6^4x^2(-2)^4+C_6^5x(-2)^5+C_6^6x^0(-2)^6

=x^6-12x^5+60x^4-160x^3+240x^2+192x+64


(3x+2)^4=C_0^4×(3x)^4×2^0+C_4^1×(3x)³×2¹+C_4^2(3x)²×2²+C_4^3(3x)¹×2³+C_4^4×(3x)^0×2^4
=81x^4+216x^3+216x²+96x+16

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 14:55

Une erreur de signe  le terme en x est négatif  (-2)^5=-32

d'accord pour (3x+2)^4

Développement : binôme de Newton .

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 15:06

Ah oui donc
x^6-12x^5+60x^4-160x^3+240x^2-192x+64

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 15:10

Oui il n'y avait pas de problème  
question 2

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 15:14

Ok

2)b En déduire le nombre de sous ensembles à n éléments.

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 15:16

2) a-

(x+1)^n=C_0^n\,x^n+C_1^n\,x^n-1....+C_3^n\,x^n-3...


\large C_n^2=\dfrac{A_n^2}{2!}=\dfrac{n×(n-1)}{2×1}=\dfrac{n²-n}{2}

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 15:23

Non  d'une façon générale vous avez :

(a+b)^n=C_n^0a^n+C_n^1a^{n-1}b+\dots+ C_n^{n-2}a^2b^{n-2}+ C_n^{n-1}ab^{n-1}    + C_n^nb^n

a=x et b=1

ce qui donne :

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 15:24

2b) il y a donc n sous ensembles à n éléments .

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 15:27

Lorsque vous utilisez LaTeX  pour des puissances ou des exposants   s'il y a plus d'un terme il faut les mettre entre accolades

2^x-1 s'écrira  2^x-1

2^{x-1} s'écrira  2^{x-1}

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 15:28

Non dans la relation que vous n"avez pas écrite faites x=1

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 15:42

Je ne comprends pas , pourriez vous m'aider à comprendre ?

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 15:51

(a+b)^n=C_n^0a^n+C_n^1a^{n-1}b+\dots+ C_n^{n-2}a^2b^{n-2}+ C_n^{n-1}ab^{n-1}    + C_n^nb^n

on remplace a par x et b par 1

(x+1)^n=C_n^0x^n+C_n^1x^{n-1}\times 1+\dots+ C_n^{n-2}x^2\times 1^{n-2}+ C_n^{n-1}x\times 1^{n-1}    + C_n^n 1^n

maintenant on simplifie

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 15:52

2-a)
(x+1)^n=C_n^0\,x^n+C_n^1\,x^{n-1}....+C_n^3\,x^{n-3}...

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 15:58

il  faut aller jusqu'au bout

(x+1)^n=C_n^0x^n+C_n^1x^{n-1}+\dots+ C_n^{n-2}x^2+ C_n^{n-1}x    + C_n^n \times 1

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 16:04

hekla @ 11-01-2020 à 15:58

il  faut aller jusqu'au bout

(x+1)^n=C_n^0x^n+C_n^1x^{n-1}+\dots+ C_n^{n-2}x^2+[ C_n^{n-1}]    + C_n^n \times 1


Pourquoi n-1 je croyais que çà devrait être n-3

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 16:13

On écrit tous les coefficients binomiaux   par ordre croissant

donc C_n^0, \; C_n^1, \; \dots ,\;  C_n^{n-1}, \; C_n^n


Pour n=5 vous avez   C_5^0=1\quad C_5^1=5\quad C_5^2=10\quad C_5^3=10\quad C_5^4=5\quad C_5^5=1

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 16:20

Je vois que çà décroît à partir de C_5^4


Pourquoi ?

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 16:22

C_n^p=C_n^{n-p}

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 16:24

Choisir de prendre p objets revient au même que de choisir n-p objets à laisser

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 16:26

Ah d'accord .

(x+1)^n=C_n^0x^n+C_n^1x^{n-1}+\dots+ C_n^{n-2}x^2+ C_n^{n-1}x    + C_n^n

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 16:30

Là  d'accord

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 16:32

Ok , comment déterminer le nombre de sous ensembles à n éléments ?

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 16:34

Ou si vous manipulez les  \displaystyle \sum

\displaystyle (x+1)^n=\sum_{p=0}^{p=n} C_n^px^{n-p}

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 16:37

Ok , le nombre de sous ensembles à n éléments dépend de n .

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 16:38

Il y a ceux qui ont 0 élément soit 1

Il y a ceux qui ont 1 élément soit C_n^1
Il y a ceux qui ont 2 éléments soit C_n^2

Il y a ceux qui ont n-1 éléments soit C_n^{n-1}
Il y a ceux qui ont n éléments soit C_n^n

et vous effectuez la somme

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 16:52

Ok .

Donc 1+C_n^1+Cn^2+Cn^{n-1}+C_n^n

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 16:54

Oui aux défauts d'écriture près

mais quel lien avec 2 a) ?

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 17:04

Je ne comprends pas quelque chose , les degrés de x dépendent de n du coup il devrait avoir n sous ensembles à n éléments non ?

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 17:16

???? Reprenons l'exemple avec n=5

On a vu que (x+1)^5=x^5+5x^4+10x^3+10x^2+5x+1

nombre de sous-ensemble à 0 élement  1
nombre de sous-ensembles à 1 élement  5
nombre de sous-ensembles à 2 élements 10
nombre de sous-ensembles à 3 élement  10
nombre de sous-ensembles à 4 élements  5
nombre de sous-ensembles à 5 élements  1

TOTAL 1+5+10+10+5+1=32=(1+1)^5= C_0^0+C_5^1+C_5^2+C_5^3+C_5^4+C_5^5

Que proposez-vous pour la généralisation ?

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 17:29


(x+1)^n=C_n^0x^n+C_n^1x^{n-1}+\dots+ C_n^{n-2}x^2+ C_n^{n-1}x    + C_n^n

Posté par
Othnielnzue23re : Développement : binôme de Newton . 11-01-20 à 17:36

Que représentent les points et pourquoi avant ceux ci on a (n-1) et après eux on a n-2 ?

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 17:41

Non vous donnez le résultat de la question 2 a)  on veut

C_n^0+C_n^1}+\dots+ C_n^{n-2}+ C_n^{n-1} + C_n^n

En liaison avec le résultat de 2 a)

C_n^0\times 1^n+C_n^1\times 1^{n-1}+\dots+ C_n^{n-2}\times 1^2+ C_n^{n-1}\times 1  + C_n^n= ?

Posté par
heklare : Développement : binôme de Newton . 11-01-20 à 17:48

Il faut prendre les mêmes éléments   les termes sont écrits dans l'ordre décroissant des puissances de x


j'ai écrit le terme d'exposant n et celui d'exposant  n-1 par conséquent les deux premiers.
Comme on ne peut pas les écrire tous,   on peut faire le choix   d'écrire les trois derniers.
  Les deux entiers précédents n sont n-1 et n-2
ce qui correspond aux coefficients des termes de degré 2, 1 et 0

1 2 3 +


Rechercher
Menu
Espace membre
6 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1742 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !