Inscription / Connexion Nouveau Sujet
Devoir a rédiger
Bonjour je suis vraiment nul j'ai besoin d'une personne qui peut m'aidez a faire cette exercice svp. Tout est en pièce jointe je vous remercie 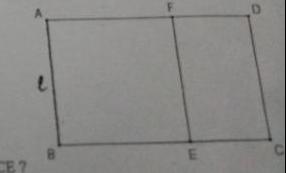
* modération> Image recadrée, sur la figure uniquement ! Si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum maxiloup,  *
*![]() Sujet ancien- ne plus donner ce lien-merci (Clique sur ce lien)
Sujet ancien- ne plus donner ce lien-merci (Clique sur ce lien)
La prochaine fois , essaie de choisir un titre plus explicite, lire Q08 ![]() [lien]**
[lien]**
Platon affirmait : « Les nombres sont le plus haut degré de la connaissance.. Le nombre de la connaissance ». Ce « nombre est le nombre d'or qui possède de très nombreuses propriétés. En mathématiques, le nombre d'or, noté( 0 barré) est défini comme la racine positive de l'équation : x ^ 2 - x - 1 = 0 .
1.Déterminer la valeur exacte du nombre d'or puis une valeur approchée à 0,01 près.
2. Justifier rapidement que 0 barrer^ 2 = 0 barrer + 1 En déduire la relation 1/0 barrer = 0 barrer - 1
Remarque : Pour calculer le carré du nombre d'or , il suffit de lui ajouter 1. Pour calculer l'inverse du nombre d'or , il suffit de lui retrancher 1.
3. Rectangle d'or. On appelle rectangle d'or un rectangle dont le quotient de la longueur par la largeur est égal à 0 barré. On suppose que le rectangle ABCD représenté ci -contre est un rectangle d'or.
On pose AB = e . Exprimer la longueur AD en fonction de e et 0 barrer . On enlève au rectangle ABCD le carré ABEF . Montrer que . Que peut EF/FD= 0 barrer. Que peut on en déduire pour le rectangle FDCE ?
** image supprimée, recadrée sur la seule figure (photos de textes interdites) **
*** message déplacé ***
Ce n'est pas "une infinité de nombre" , c'est un nombre.
Il s'agirait de lire le texte de l'exo :
En mathématiques, le nombre d'or, noté( 0 barré) est défini comme la racine positive de l'équation : x ^ 2 - x - 1 = 0
Bonjour je fait appelle a vous car je n'arrive pas du tout a trouver les réponse. Voici l'énoncé et les question
Platon affirmait : « Les nombres sont le plus haut degré de la connaissance.. Le nombre de la connaissance ». Ce « nombre est le nombre d'or qui possède de très nombreuses propriétés. En mathématiques, le nombre d'or, noté( 0 barré) est défini comme la racine positive de l'équation : x ^ 2 - x - 1 = 0 .
1.Déterminer la valeur exacte du nombre d'or puis une valeur approchée à 0,01 près.
2. Justifier rapidement que 0 barrer^ 2 = 0 barrer + 1 En déduire la relation 1/0 barrer = 0 barrer - 1
Remarque : Pour calculer le carré du nombre d'or , il suffit de lui ajouter 1. Pour calculer l'inverse du nombre d'or , il suffit de lui retrancher 1.
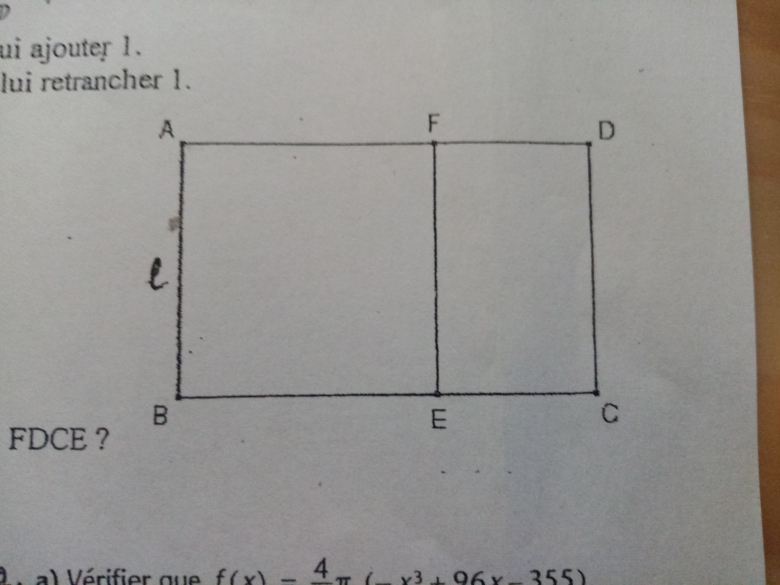
3. Rectangle d'or. On appelle rectangle d'or un rectangle dont le quotient de la longueur par la largeur est égal à 0 barré. On suppose que le rectangle ABCD représenté ci -contre est un rectangle d'or.
On pose AB = e . Exprimer la longueur AD en fonction de e et 0 barrer . On enlève au rectangle ABCD le carré ABEF . Montrer que . Que peut EF/FD= 0 barrer. Que peut on en déduire pour le rectangle FDCE ?
Pour la 1) jai trouvé : la valeur exacte est de (1V5/2) et la valeur approcher est de 1,618
Pour la 2) j'ai fait (V5+1/2)=5+2V5+1/4=V5+3/2. ce qui me donne 0 barré ^2= 0 barré +1
Et j'ai fait 1+1/0 barré = 0 barrée
0 barré-1+1/0 barré = 0
Pour la 3 je ne serai réellement pas lq faire.
Merci de l'aide
*** message déplacé ***
Bonsoir,
Pour la 3) :
AB = e, AD = e , FD = e
, FD = e - e = e(
- e = e( -1)
-1)
Comme on a EF = e, on en déduit EF/FD = 1/( -1)
-1)
Avec la question 2) tu peux montrer que 1/( -1) =
-1) = 
Donc ECDF est également dans la proportion du nombre d'or, mais orienté perpendiculairement.
*** message déplacé ***
C'est a dire que je devrai mettre 2^2-2-1
Pourquoi tu remplaces x par 2 ?
Lis le texte !
le nombre d'or est la racine positive de l'équation : x ^ 2 - x - 1 = 0




 ) :
) :

