Inscription / Connexion Nouveau Sujet
devoir de maths
Bonjour, je suis bloqué pour cette exercice, pourriez vous m'aider
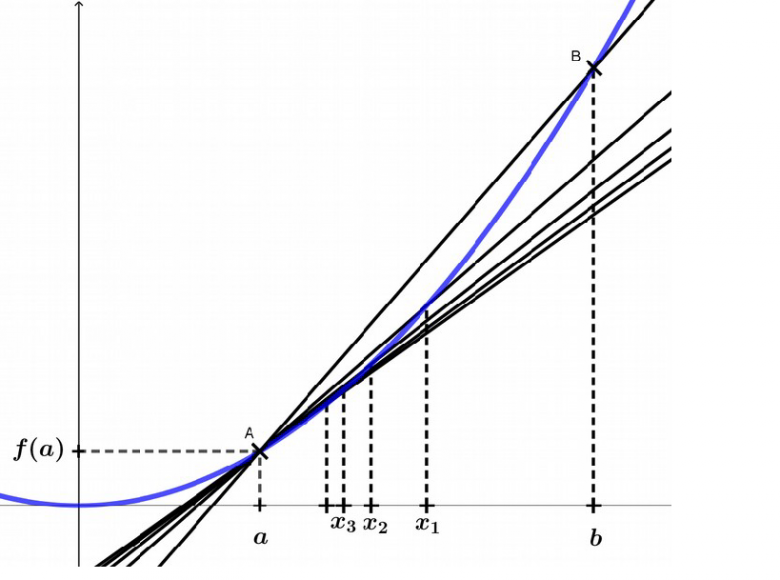
Exercice: Considérons une fonction f dérivable pour tout x∈I , où I est un intervalle ouvert, et soit [ a; b ] un intervalle inclus dans I et notons A le point de la courbe représentative Cf de f d'abscisse a et B le point d'abscisse b. On rappelle que la tangente à Cf au point A est la « position limite » des sécantes (AAn) où An sont des points de la courbe Cf , sur l'arc AB , de plus en plus proches de A lorsque n devient de plus en plus grand.
On choisit comme abscisses pour An les réels suivants : xn=a+b−an
(lorsque n tend vers +∞ , xn tend vers a car b−an tend vers 0)
Le but est de stocker dans une liste les coefficients directeurs des droites (AAn) , pour n donné par l'utilisateur.
Partie A : Partie programmation : une conjecture
Les tests se feront avec la fonction carrée définie par f (x )=x2 .
On peut définir cette fonction en langage Python comme à la ligne 1.
1) a) Donner les coordonnées du point A en fonction de a et de f (s'aider de la figure si besoin)
b) Donner les coordonnées du point An d'abscisse xn en fonction de xn et de f
c) Donner alors le coefficient directeur de la droite (AAn) en fonction de a , xn et de f
2) Compléter alors les lignes 6 et 7 du programme ci-contre, à l'aide de la partie introductive
3) Que représente la variable cd ? Que permet de faire la ligne 8 ?
4) Ecrire ce programme dans Python, puis l'exécuter
5) Afficher la liste des coefficients directeurs des sécantes sur l'intervalle [1;2] avec : a) n=10 b) n=20 c) n=100
→ Copier-coller les listes ainsi obtenues dans un fichier texte, et les envoyer par mail.
6) Vers quelle valeur semblent tendre les coefficients directeurs de la liste obtenue ?
Partie B : Vérification de la conjecture par le calcul
1) Calculer le taux d'accroissement de f : x → x² entre 3 et 3 + h , où h est un réel non nul.
2) En déduire le nombre dérivé de f en 3.
3) Quel semble être le nombre dérivé de f en un point x quelconque ? Justifier par le calcul.
1. f=lambda x:x**2
2.
3. def ListeSecantes(f,n,a,b):
4. L=[]
5. for k in range(1,n+1):
6. xk =
7. cd =
8. L.append(cd)
9. return L
Bonjour psfgt,
Carpediem te parle de
Et question 1 => tu n' as pas une figure jointe à ton exercice ? Là, c'est un peu indigeste...
Ok, c'est déjà plus clair 
Et sur quelle question bloques-tu ? (ne me réponds pas "à la question 1", stp)
non la 1 c'est bon pour la c j'ai mis:
(f(xn)-f(a))/(xn-a)
mais je ne suis pas sur, et c'est pour la 2 et la 3 que je bloc
Ta réponse a la question 1)c) est bonne (coefficient directeur).
Mais j' ai l' impression qu' il manque un morceau du puzzle, et du coup, je comprends mieux la quetion posée au début par Carpediem. Qui est ce , qui nous permettra de déterminer les abscisses x1, puis x2, puis x3 ?
Quelqu'un pour nous éclairer ? 
An sont des points de la courbe Cf , sur l'arc AB , de plus en plus proches de A lorsque n devient de plus en plus grand.
On choisit comme abscisses pour An les réels suivants : xn=a+b−an
(lorsque n tend vers +∞ , xn tend vers a car b−an tend vers 0)