Inscription / Connexion Nouveau Sujet
Devoir maison : le produit scalaire...
Bonjour !
J'ai un devoir maison de maths :
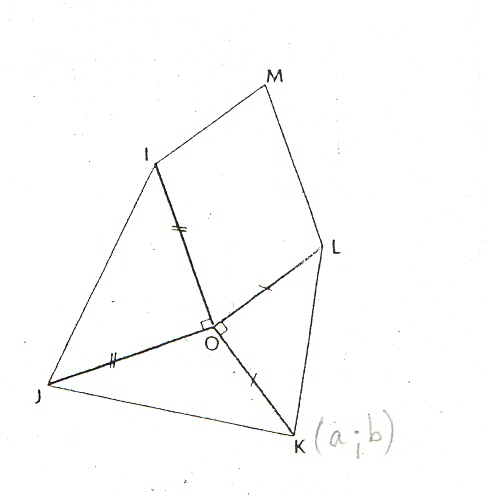
OIJ et OKL sont deux triangles rectangles isocèles tels que (OI ; OJ) = +
/2 et (OK ; OL)= +/2.
OIML est un parallélogramme. On se propose de démontrer que : IK=JL , OM=JK , (JL)est perpendiculaire à (IK) ainsi que (OM)et(JK).
a) démontrer que (OJ;Ok) + (OL;OI)=. Exprimer cos(OL;OI) en fonction de cos (OJ;OK).
J'ai répondu : comme tous les angles sont rattacher au point O, on peut considérer que la somme de ces angles sont de 2. Puisque la somme des angles (OI;OJ)+(OK;OL)=/2+ /2 =. Alors 2-(OI;OJ)+(OK;OL)=. (Oj;OK)+(OL;OI)=.
Comment rendre ma réponse moins confuse ? 
Pour exprimer cos(OL;OI) en fonction de cos (OJ;OK), il faut utiliser la propriété qui dit que l'angle iOl est égal à la moitié de jOk, Comment s'appelle t'elle ? ( du moins, si elle a un nom..)
J'espère que quelqu'un arrivera à déchiffrer mon dm ! 
Aidez moi ! merci d'avance
Bonjour
la propriété que tu as inventée n'a pas de nom .... si elle était vraie, tu pourrais lui donner ton nom !
plus sérieusement, que sais tu de cos(pi - x) ? (un des angles étant pi moins l'autre)
Ta réponse n'est pas du tout confuse .. ne change rien..
Ensuite il faut écrire que cos (pi-x)=-cosx.
cos(OL;OI) = - cos (OJ;OK).
il faut utiliser la propriété qui dit que l'angle iOl est égal à la moitié de jOk,
EN plus ce n'est pas vrai !!
OKidacc, je n'avais pas du tout pensé cos (pi-x)=-cosx.
donc cos(OL;OI) = - cos (OJ;OK). 
(lahonte)
Pour la propriété qui n'existe pas, je la prouverai un peu plus tard ...
Merci beaucoup pour vos réponses
Beh .. en fait, ça mène à rien ce que je fais ..
la question b : démontrer que IK=JL et le produit scalaire IK.JL=O en utilisant le fait que les vecteurs IK=OK-OI et JL=OL-OJ
je vois pas comment on peut dire que IK et JL sont perpendiculaires...
j'arrive à
IK.JL = (OK-OI)².(OL-OJ)²= (OK²-2OI.OK+OI²).(OL²-2OJ.OL+OJ²) mais après ça m'embrouille vite.
stop ! Quand tu écris IK.JL, il s'agit du produit scalaire (d'ailleurs, à 16:11, j'ai oublié le premier carré : IK²=||...||² etc)
Développes en utilisant la bilinéarité du produit scalaire (mot compliqué pour dire que ça se développe comme les produits (x-y)(a-b) dans IR....)
IK.JL=(OK-OI).(OL-OJ)
=OK.OL - OK.OJ - OI.OL + OI.OJ
Comment faire pour que ce soit égal à 0 ?
regardes ta figure : (OK) et (OL) orthogonales : un produit scalaire nul, continue... ensuite, pour ceux qui restent, écris les avec la déf qui fait intervenir le cos et rappelle toi du a) ....
d'accord, on arrive bien à zéro !
merci du coup de main ! encore un autre truc : pour la dernière question, on me demande de démontrer que OM.JK=O, je peux continuer avec les vecteurs OM=IM-IO et Jk=OK-OJ ?
Ayé, je l'ai démontrer! 
Bon beh merci pour avoir passer la moitié de l'après-midi à m'expliquer mon DM !
Bon, il y a encore une deuxième partie mais je la sens bien celle-ci.
Annuler
connectez vous