Inscription / Connexion Nouveau Sujet
Difficultées à rééaliser une figure
Bonjour.
Sur cette exercice je n'arrive pas à réaliser la figure demandée (question 1.c) Pouvez vous m'aidez svp. Merci d'avance.
Le plan orienté est rapporté au repère orthonormal direct (O, u, v), l'unité graphique étant 4 cm.
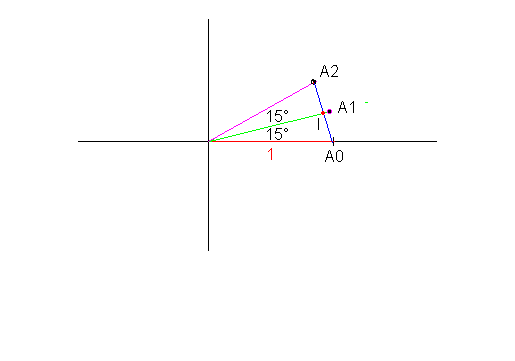
On considère les points A0 . A1 de coordonnées polaires respectives : A0 [1 ; 0] A1[1 ; pi/12]
Le point A2 est l'image du point A1 par la rotation r de centre O et d'angle pi/12
1.a. Calculer les coordonnées polaires du point A2 ; en déduire ses coordonnées cartésiennes.
b. Soit I le milieu du segment [A0 A2]. Calculer les coordonnées du point I.
c. Faire une figure.
2.a. Prouver que les droites (01) et (0A1) sont confondues.
b. Calculer les coordonnées polaires de I.
c. Déterminer cos(pi/12) et sin(pi/12) (les valeurs exactes sont exigées), sachant que V(4 + V 3 + 8) = V6 +V2.
e ici
Voici les répônces aux questions précédentes 1.a et 1.b :
1a. D'après la définition de la rotation on aura : OA2=1=OA1
et l'angle de OA2 avec OA1 sera égal à : pi/12
par conséquent l'angle de OA avec Ox sera pi/12+pi/12=pi/6
coordonnées polaires de A2(1,pi/6)
Les coordonnées cartésiennes seront donc
(cospi/6;sinpi/6)
1.b
x2 = cos(pi/6) = rac(3)/2
y2 = sin(pi/6) = 1/2
xI = = (x0 + x2) / 2 = [2 + rac(3)] / 4
yI = (y0 + y2) / 2 = 1/4
Ou est ta difficulté dans la construction ?
Pour le point A0 :
Il a pour coordonnée polaire [1;0] ce qui signifi que et
. Autrement dit , le point A0 a pour coordonnée cartésiennes (0;1)
Pour le point A1
Il a pour coordonnée polaires donc on a :
et
donc tu traces un arc de cercle de centre 0 et de rayon 1 et le point
de coordonnées cartésiennes
Pour le point A2 , tu prends ton compas puis tu trace un arc de cercle de centre O , de rayon 1 et tu fais un angle de 90° et tu as ton point A_{2}

bonjour,
je suppose que ce qui te pose problème, c'est de représenter A1.
en fait, il faut d'abord représenter A2, qui se fait très simplement:
représente un triangle équilatéral OA0B de sorte qu'il soit direct (B doit être au dessus de l'axe des absisses).
trace la bissectrice de l'angle (). Cette bissectrice coupe le cercle unité au point A2, car les bissectrice sépare les angles en 2 angles égaux (et
maintenant, il te reste plus cas refaire le travail (tracer la bissectrice) pour cet angle ().
La nouvelle bissectrice coupe le cercle unité au point A1.
qu'en au point I, il se trouve à l'intersection des droites (OA1), at (A0A2)
voilà
excuse moi, pour le point I, on ne peut pas raisonner ainsi, car il faut le démontrer après, donc tu dois tracer la médiatrice de [A0A2].
Oups , autant pour moi , on a effectivement :
Et :
Ainsi que :
Bon , daccord , c'est assez dur à trace mais bon ... 

je me permets de soulever une autre erreur, je pense, pourquoi tu fait un quart de tour pour tracer A2? ta rotation n'a pas un angle de 90° dans le sens direct, ni indirect. De plus, non seulement c'est une erreur, mais tu obtiens 2 points et pas un unique.

Arf oui , j'ai encore confondu pi/12 et pi/2 .. Jdevrai mettre des lunettes moi 
Désolé encore une fois 

Remarque sur le dessin: un angle de Pi/12 = 15° est construtible sans difficulté comme suit:
Un triangle équilatéral -> angle de 60°
On divise cet angle en 2, puis en deux au compas et à la latte -> 15° construit exactement.
Ne pas oublier pour la construction que OA1 = OA2 = OA3 = 1 (donc 4 cm).