Inscription / Connexion Nouveau Sujet
Distance d'un point à une droite
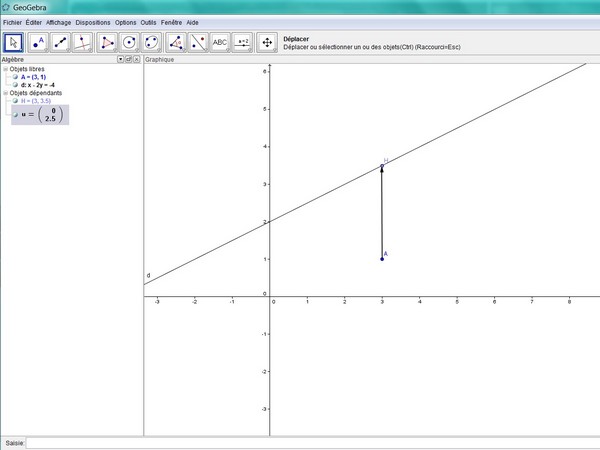
Voilà j'ai un problème de débutante, je connais le résultat mais pas la façon de l'obtenir j'aurais besoin d'aide s'il vous plait. Ci-joint la configuration faite par géogébra
Voici l'énoncé :
On considère la droite d d'équation x-2y+4=0 et le point A(3;1). Le point A se projette orthogonalement sur d en H.
1) Si le point H a pour abscisse a quelle est son ordonnée ?
2) En écrivant que (vecteur AH) est orthogonal à d, déterminer a.
3) En déduire la distance AH qui est la distance de A à d.
Bonjour !.... à toi aussi 
Le point A se projette orthogonalement sur d en H.
ton dessin est faux...(AH) doit être perpendiculaire à la droite (d)
H est sur (d) donc ses coordonnées vérifient l'équation de (d)
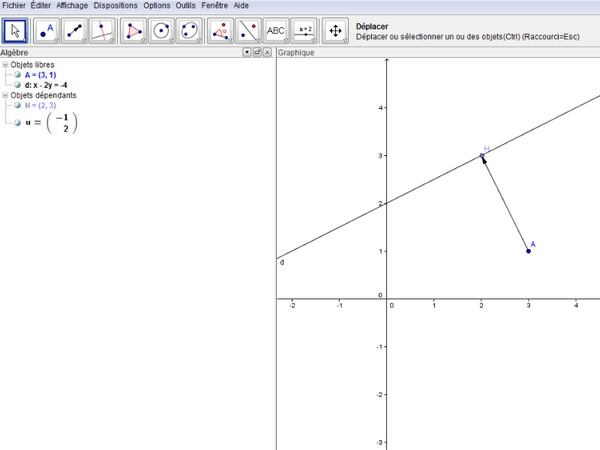
Merci mais j'ai toujours le même problème même en ayant une figure correcte : je connais les coordonnées de H(2;3) grâce à géogébra mais je ne vois vraiment pas comment les obtenir à partir de l'équation ou du moins comment répondre aux questions.
Mais je sais que les coordonnées de H vérifient l'équation de d : x-2y+4=0 
2-2*4+4=0.
on te dit
le point H a pour abscisse
tu dois calculer l'ordonnée en fonction de
avec l'équation de d
ensuite fais ce qu'on te dit....
1) Si le point H a pour abscisse a quelle est son ordonnée ?
2) En écrivant que (vecteur AH) est orthogonal à d, déterminer a.
3) En déduire la distance AH qui est la distance de A à d.
Donc pour le 2 je peut écrire :
H projeté orthogonal de A sur d AH
d AH orthogonal à d.
Mais comment calculer a ?
Pour le 3) je connais les coordonnées de H à l'aide de géogébra donc je pose 
(xb-xa)²+(yb-ya)² et je trouve 5. Est-ce juste ?
Pour le 3) je connais les coordonnées de H à l'aide de géogébra
non, ce n'est pas ce qu'on te demande...
Calcule les coordonnées de
trouves un vecteur directeur
écris que
tu trouveras une équation
tu résous cette équation et tu auras l'abscisse de H, tu en déduiras l'ordonnée et tu pourras alors calculer AH
Vecteur directeur de la droite (d) = (2;1)
Comment calculer les coordonnées de AH en fonction de a alors que je ne connais pas a ?
si tu as lu ce que je t'ai écrit à 18:43 c'est simple.....
tu as
donc
écris que le produit scalaire est nul
tu es capable de faire ça ?
tu trouveras une équation, résous la pour avoir l'abscisse de H
J'ai trouvé une équation et j'aimerais une validation avant de continuer : ax-3x+a/2*y+y-3a-a/2-8=0
C'est juste ?
effectivement...je ne sais pas comment tu as trouvé cette chose 
c'est pourtant simple il suffit de calculer le produit scalaire....pour cela il faut l'apprendre
Tu dois absolument savoir :
Dans un repère orhonormé
si
alors
ici tu as
et
donc
d'où l'équation
tu résous et tu dois trouver
puis l'ordonnée de H :
et les coordonnées de H(2;3) que tu devrais vérifier sur le dessin
Annuler
connectez vous