Inscription / Connexion Nouveau Sujet
dm
Bonjour
Pourriez vous m'aider à débuter mon dm
Soit f une fonction définie sur l'ensemble des réels par f(x)= ax3+bc2+cx+d ou a,b,c et d sont des réels. On note (C) se courbe représentative.
On sait que:
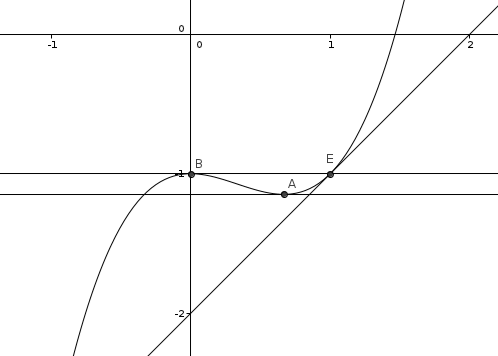
(C) admet au point A d'abscisse 2/3 une tangente horizontale
La droite d'équation y=-1 est tangente à (C) au point B d'abscisses 0
(C) admet au point E d'abscisse 1 une tangente parallèle à la droite d'équation y=x+3
déterminer les réels a, b, c et d
Merci d'avance
Hello,
quand il y a une histoire de tangente il y a sûrement la dérivée qui intervient.
rappel : le nombre dérivé f'(x) est le coefficient directeur de la tangente à la courbe au point d'abscisse x.
Prenons :
(C) admet au point A d'abscisse 2/3 une tangente horizontale
il faut traduire ça par
Tu traduis les autres conditions et tu auras ainsi un système d'équations en a, b, c et d à résoudre.
PS : tu as trois conditions dans ton exo...es tu sûre qu'il n'y en a pas une quatrième ?
Exact c'est la seconde condition...n'est-ce pas ? Non seulement la tangente doit être horizontale mais en outre
. Sauf distraction.

Bonjour dhalte
donc je dois commencer par faire f'(2/3)=0 mais je ne sais pas comment faire pour résoudre cette equation :/

je te montre.
je calcules d'abord f'(x) :
f'(x)=3ax2+2bx+c.
ensuite je remplace x par 2/3 et j'écris que cela fait 0 :
3a(2/3)2+2b(2/3)+c=0
3a(4/9)+(4/3)b+c=0
(4/3)a+(4/3)b+c=0
en multipliant par 3
4a+4b+c=0.
Voilà ta première équation en a, b, c et d.
Tu en a trois autres à trouver et tu auras ton système que tu pourras résoudre pour trouver a, b, c et d. Et là ce sera fini.
OK ?
Je te rappelle que la seconde condition donne deux équations f(0)=-1 et f'(0)=0......et relis bien les posts précédents.
Normalement c'est facile maintenant mais bon si tu as des problèmes je traine dans le coin....donc tu peux poser des questions.