Inscription / Connexion Nouveau Sujet
dm
Bonjour, j'ai un dm en maths et je suis bloquée dans une question :
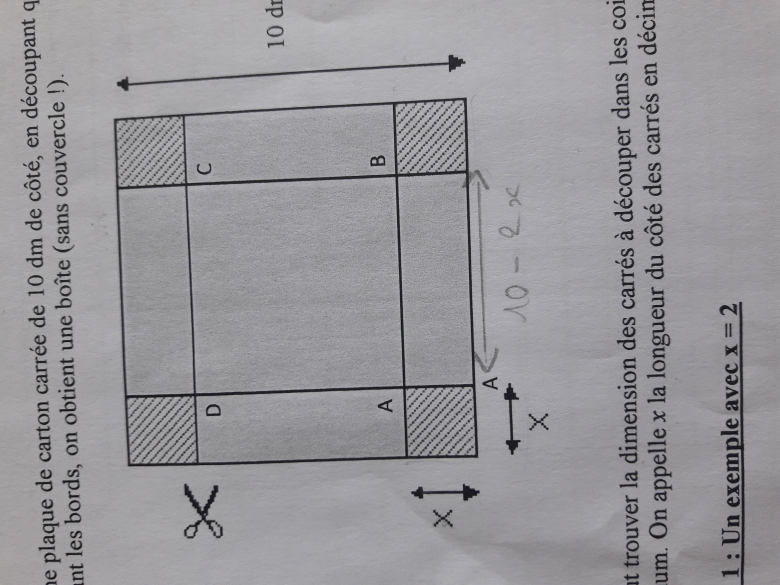
On veut trouver la dimension des carrés à decouper dans les coins pour obtenir une boîte dont le volume sera maximum.On appelle x la longueur du côté des carrés en décimètre.
•Partie 1 : Un exemple avec x=2
a)Lorsque x=2, montrer que la longueur AB est 6 dm .
Donc moi j'ai fait : 10-2×2=6dm
b)En déduire l'aire du carré ABCD.
J'ai fait: 6×6=36dm au carré
c)Sachant que le volume du parallélépipède est V = aire de la base×hauteur,montrer que le volume de la boîte est V =72 dm3
J'ai calculer le volume: 36×2=72dm3
•Partie 2: Cas général
Voici la question qui me pose soucie:
1) Quelle est la plus grande valeur possible de x?
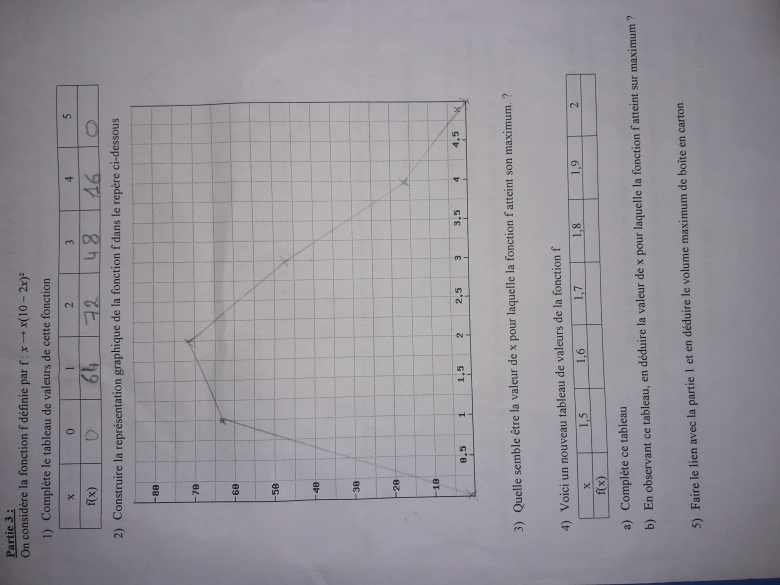
Donc moi pour commencer jai fait un tableau.
Une ligne pour x: 1,2,3,4,5
Et une ligne pour f(x)
Je n'arrive pas à completer mon tableau et quel calcule.
Je vous en prie de m'aider  Merci
Merci
Bonjour
Ton énoncé est-il complet ? La partie 2 ne comporte qu'une seule question ?
1) Quelle est la plus grande valeur possible de x?
Si x=5, que reste t-il de la base ?
Alors il restera 0 donc la valeur maximal est 5
Voici les autres questions de la Partie 2:
2) a) Exprime en fonction de x la longueur AB du fond de la boîte
b) En déduire, l'expression de l'aire de ABCD, correspondant au fond de la boîte, en fonction de x
d)En déduire, l'expression du volume de la boîte en fonction de x sachant que la formule pour le volume d'un parallélépipède est V=aire de la base×hauteur
0<x<5 car si x=0 et x=5 la boîte n'existe plus
La valeur de AB est écrite sur ton dessin (valeur du côté de la base)
L'aire de la base de la boîte ABCD est l'aire d'un carré, donc son aire est côté*côté et son volume aire de la base*hauteur x
Anonyme01091
Utilise * pour multiplié par pour le distinguer de la lettre x
(10-2x)(10-2x)=(10-2x)2 que je pense peut-être inutile de développer
et le volume V=x(10-2x)2
ne pas oublier de taper 2 qui se place entre les 2 balises sup. Tu peux vérifier si c'est bien en cliquant sur Aperçu.
Daccord  merci encore pour votre aide!
merci encore pour votre aide!
Par contre jai la partie 3. Pouvez vous me dire si il ya une erreur
Quelle partie 3 ? Si tu ne l'écrit pas comment la deviner ? Je ne suis pas extralucide.
Que de temps perdu en ne recopiant pas d'entrée l'énoncé complet.
Je n'avais pas vu ton dernier envoi
La fonction f(x) du volume est du 3ème degré et est une courbe qui ne peut pas se tracer par segments
pour plus de précision, il faudrait calculer f(x) avec une valeur comprise entre 1,5 et 2 et aussi une valeur comprise entre 2 et 2,5 (par exemple 1,75 et 2,25) pour savoir si pour x=2 on a bien le maximum.
Voici la question 4 je viens de le faire, pour la question b jai repondu :
F est maximal pour x=1,7
Et pour la 5 je ne comprend pas comment faire le lien mais j'ai deduis le volume maximum:
•J'ai calculer l'aire de la base: (10-2*1,7)*(10-2×1,7)=43,56
•Ensuite le volule: 43,56×1.7=74,052

Anonyme010918
Oui, mais il manque les unités.
Note que pour une prochaine fois, si tu ne recopies pas ton énoncé complet d'entrée au lieu de le distiller au compte goutte, je ne répondrai pas.