Inscription / Connexion Nouveau Sujet
DM: comparaison de fonctions+ cône circonscrit à une sphère
1- cône circonscrit à une sphère
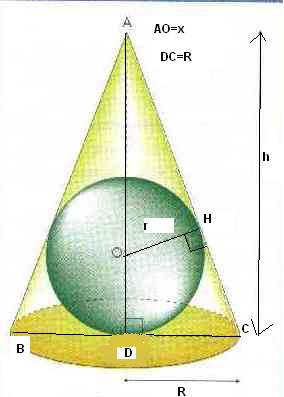
S est une sphère de centre O de rayon R. On souhaite inscrire cette shpère dans un cône de révolution dont le volume V est le plus petit possible, quelles doivent être les dimentions de ce cône ?
a- pour répondre on pose AO=x. vérifier que V=1/3(pi)R²((X+r)²/x-R)
b- démontrer que le cône de volume minimal est obtenu lorsque x=3R. quelle est alor la hauteur de ce cône ? le rayon de sa base ?
->normalement il y a une figure j'espère que vous pourrez m'aider sans. la a) et faite mais je bloque sur la b)
2-comparaison de fonctions
les fonctions f et g sont définies sur R respectivement par f(x)=x^4-3x+1 et g(x)=2x^3-3x-1
a- trouver et simplifier d(x)=f(x)-g(x)
b- vérifier que d est dérivable sur R et calculer, pour tout x de R, d'(x)
AIDEZ MOI SVP!
bonjour
pour l'exo 1 c'est qoui A (je suppose le sommet du cône)? c'est quoi x?
2) a) d(x)=(x^4-3x+1)-(2x^3-3x-1)
=x^4-2x^3+2
b) d est la différences de deux polynômes qui sont dérivables sur IR donc d est dérivable
d'(x)=4x^3-6x²
=2x²(2x-3)
donc d' est du signe de 2x-3
d'(3/2)=0 et d'(0)=0
d'(x)>0 sur ]3/2,+oo[ et d'(x)<0 sur ]-oo,3/2[
oui A et le sommet du cône et X et la longueur entre le centre de la sphère et le sommet du cône , x=AO
je reviens au 1)
un plan méridonal coupe le cone et la sphère en un triangle ABC et un cercle de centre O et de rayon R.
le cercle est tangent au traingle aux point B' et C' et H le pied de la hauteur issue de A au triangle.
je pose b le rayon du cône. la base du triangle a pour longueur 2b
si x=AO alors la hauteur du cone est h=x+R
le volume du cone est V(x)=(1/3)Pib²h
=(1/3)Pib²(x+R)
les triangles AOC' et ABH sont semblables car ils ont deux angles deux à deux égaux.(un angle droit et un angle commun A).
donc
BH/OC'=AB/AO
BH=b
OC'=R
AB=V(b²+x²) ;V()=racine carré
AO=x
donc
b/R=V(b²+(x+R)²)/x
donc
b²/R²=(b²+(x+R²)/x²
b²(x²-R²)=R²(x+R)²
b²=R²(x+R)/(x-R) ; en supposant x>R
donc
V(x)=(Pi/3)R²(x+R)²/(x-R)
b)V'(x)=(Pi/3)R²[2(x+R)(x-R)-(x+R)²]/(x-R)²
=(Pi/3)R²[2x²-2R²-x²-2xR-R²]/(x-R)²
=(Pi/3)R²[x²-3R²-2xR]/(x-R)²
V'(x)=0 ssi x²-3R²-2xR=0
c'est une équation de second degré en x
Délta=4R²+12R²=16R²
x=(2R+4R)/2=3R ou x=(2R-4R)/2=-R ce dernier cas n'est possible car x>0
donc x=3R
pour cette valeur V'(X)=0 et le signe de V'(x) est
V'(x)>0 ssi x>3R et donc V est croissante sur ]3R,+oo[
V(x)<0 ssi 0<x<3R donc V est décroissante sur ]0,3R[
donc V atteind bien sa valeur minimale en x=3R
ha ok alor dans le 2b- on ne prend que la valeur possitive ... merci de ton aide, si un autre truk coince dans mais autre exercice , je l'écrirai ici en espérant une réponse.
encore merci, a bientot.