Inscription / Connexion Nouveau Sujet
DM d'entrée en 1ere S Fonctions
Sujet :
EBF est un triangle isocèle inscrit dans le carré ABCD de côté 5cm avec DE=DF . figure : 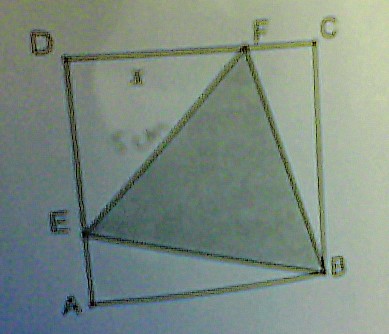
On propose de trouver la longueur de EF pour que le triangle EBF soit équilatéral et de construire ce triangle. On appelle x la longueur DF .
A- Valeur approchée de EF
1) Dans quelle intervalle l se situe le nombre réel x ?
2)Exprimer la longueur EF en fonction de x , on notera f(x)
3) Montrer que la longueur BF , notée g(x) est égale à g(x)=racine carré de 50-10x+x²
B-Calcul de EF
1) Montrer en utilisant les résultats de la partie A , que le problème se ramène à résoudre dans l'intervalle l l'équation 50-10x+x² = 2x²
2) Montrer que cette équation peut se ramener à (x+5)² = 75
3) Résoudre l'équation dans l , puis déterminer la longueur EF et comparer au résultat obtenu dans la partie A
C-construction de triangle EBF - Vlaur de cos(15°)
1) Justifier que la droite (BD) est la bissectrise de l'angle EBF.
2) a) Lorsque le triangle EBF est équilatéral, quelle est alors la messure de l'angle CBF ?
b)Exprimer la longeur BF en fonction de cos CBF.
c) En utilisant les résultats des parties A et B, donner la valeur exacte des cos(15°)
Merci de bien vouloir me repondre dans un delais assez rapide merci encore
♥
édit Océane : image placée sur le serveur de l' merci d'en faire autant la prochaine fois
merci d'en faire autant la prochaine fois 
J'espere que ce n'est pas un probleme d'utiliser le meme post pour le meme probleme.
J'ai le meme exercice et j'ai avance jusqu'a la partie C (+le petit c de la partie B) sur laquelle je bloque completement.
Voic ou j'en suis sur le reste. Si quelqu'un pouvait valider aussi ce serait bien. Merci.
Partie A:
1- I[0;5]
2-a Theoreme de Pythagore
DE=DF=x
EF^2=x^2+x^2
EF=xracine2
f(x)= xrac2
2-b) meme methode
FC=(5-x) et CB=5
Donc BF^2=(5-x)+5^2
BF=Rac50-10x+x^2 = g(x)
Partie B
a)En utilisant Pythagore pour BFC et EDF et sachant que EBF est equilateral on a EB=EF=FB
EF^2=FB^2
2[/sup]=50-10x+[sup]
b) 2[/sup]=50-10x+[sup]
[/sup]+10x-50=0
et
(x+5)^2=75
[sup]+10x+25=75
[sup][/sup]+10x-50=0
c) I[0:5] et a partir de la je bloque completement
Merci d'avance de votre aide
visiblement j'ai du mal a utiliser les symboles ou j'ai fait une erreur de frappe, je reposte:
Partie A:
1- I[0;5]
2-a Theoreme de Pythagore
DE=DF=x
EF^2=x^2+x^2
EF=xracine2
f(x)= xrac2
2-b) meme methode
FC=(5-x) et CB=5
Donc BF^2=(5-x)+5^2
BF=Rac50-10x+x^2 = g(x)
Partie B
a)En utilisant Pythagore pour BFC et EDF et sachant que EBF est equilateral on a EB=EF=FB
EF^2=FB^2
2x^2=50-10x+x^2
b) 2x^2=50-10x+x^2
x^2+10x-50=0
et
(x+5)^2=75
x^2+10x+25=75
x^2+10x-50=0
c) I[0:5] et a partir de la je bloque completement
Merci d'avance de votre aide
A- Valeur approchée de EF
1) Dans quelle intervalle l se situe le nombre réel x ?
Si on considère un triangle plat, l appartiens à ]0;5] Sinon [0;5]
2)Exprimer la longueur EF en fonction de x , on notera f(x)
Il faut utiliser le théorème de Pythagore, x=DE=DF
Et donc nous avons : EF²=2x²
Par conséquent EF est égale au produit de x par la racine de 2.
3) Montrer que la longueur BF , notée g(x) est égale à g(x)=racine carré de 50-10x+x²
AB=BC+CD+DA=5 et FC=(DC-DF)=(5-x), il faut alors réutilisé le théorème de Pythagore.
BF²=(5-x)²+5²
BF²=25-10x+x²+25
BF²=x²-10x+50
BF est donc égal a la racine carré de (x²-10x+50).
B- Calcul de EF
1) Montrer en utilisant les résultats de la partie A , que le problème se ramène à résoudre dans l'intervalle l l'équation 50-10x+x² = 2x²
Etant donné que DE=DF; EA=FC et AB=BC+CD+DA=5
EB=BF; Il faudra donc chercher la solution tel que BF soit égal à EF
Et donc la racine carré de (x²-10x+50) égal au produit de x par la racine de 2.
=) x²-10x+50=2x² (Mise au carré de chaque côté de l'inéquation.
2) Montrer que cette équation peut se ramener à (x+5)² = 75
x²-10x+50=2x²
x²-10x+50-2x²=0
-x²-10x+50=0
x²+10x-50=0 Il faut chercher à factoriser. 10x = 2*5x (rappel : (x+a)=x²+2xa+a²) or 5²=25 donc il faut ajouter 75
x²+10x-50+75=0+75
x²+10x+25=75
(x+5)²=75
3) Résoudre l'équation dans l , puis déterminer la longueur EF et comparer au résultat obtenu dans la partie A
(x+5)²=75
x+5="racine de"(75)
x=5"racine de"(3)-5
x=5("racine de"(3)-1)
S={5("racine de"(3)-1)}
C- construction de triangle EBF - Valeur de cos(15°)
1) Justifier que la droite (BD) est la bissectrice de l'angle EBF.
Il faut utiliser la relation DC/DF=DA/DE=AC/EF et comme nous sommes dans un carré, l'intersections des diagonales est en leurs milieu et donc BD coupe EF en sont milieu.
2) a) Lorsque le triangle EBF est équilatéral, quelle est alors la mesure de l'angle CBF ?
angle EBF est de 60° comme triangle équilatéral et ABC=90° EAB et FCB triangles dont les côtés sont de même longueurs.
"angle"ABE="angle"FBC=(90-60)/2=15°
"angle"ABD="angle"DBC=45°
"angle"ABD="angle"DBC=45-15=30°
b)Exprimer la longueur BF en fonction de cos CBF.
Cos(FBC)=CB/BF
Cos(FBC)=5/BF
BF=5*Cos(FBC)
c) En utilisant les résultats des parties A et B, donner la valeur exacte des cos(15°)
Il faut reprend la réponse du petit 3 de la partie B
Cos(15°)=5("racine de"(3)-1)
En espèrant avoir pût vous aider
Excuser moi mais je n'ai pas compris la partie 3/
Du II. On peux juste m'expliquer le passage de x+5='racine de'75
Et comment par la suite on retrouve le resultat du I. qui est environ égal a 3.6
J'ai également eu cet exercice comme devoir maison, cependant je ne comprends pas la question 2c) de la partie C, vous avez marqué que cos(15) = 5*((racine de 3)-1), alors qu'en vérifiant à la calculatrice, cette égalité est fausse...
Quelle est donc la bonne réponse ?
J'ai le même devoir maison de Mathématique et je n'arrive pas les questions de l'exercice deux Partie B.
Merci d'avance de votre aide.
Bonjour tout le monde ,
juste une petite question : pensez vous normal que mon frere ( en seconde ) doit faire ce meme dm ?
merci d'avance et dsl du derrangement
Bonjjours a tous,
Moi aussi j'ai eu ce DM et je suis en seconde...
J'ai du avoir recour amon frère, 3 amis et 2 sites pour comprendre quelques chose. Je ne l'ai même pas encore finis et je galère trop.
Enfin en tout cas merci pour l'aide !
Et désolé pour cette parenthèse inutile ! ^^
J'ai le même Dm je ne comprend rien a la partie C :S Quelqu'un peut m'aider ? Sa serais super simpas ! Merci d'avance


