Bonsoir,
ça ressemble à un problème d'optimisation. Tu choisis un inconnu (par exemple la longueur d'un des bouts) et tu établis une fonctions qui te donne l'aire totale. Tu dérive la fonction et tu cherches un maximum.

Bonsoir ,
Si x la longueur qui va former le carré , 1-x sera le périmètre du cercle .
Aire du carré : (x/4)² .
Rayon du cercle : r=(1-x)/(2)
Aire du cercle  : r².
la somme des aires sera une expression du 2nd d° en x , dont le coeff de x² est >0  ---> parabole à minimum pour x = ...
bonne nuit .

Merci je vais aller me coucher cette exercice demande beaucoup de réflexion, donc je met sa sous forme de trinome donc

(x/4)² + (1-x)/(2Pi) pi r² = x

j'espère que tu as bien dormi .
la somme des aires est :
(x/4)²+(1-x)²/(4)
cette expression sera minimum si sa dérivée est nulle .
Développe , dérive , annule cette dérivée --> d'où x .

Bonsoir,

Oui merci j'ai (1x/4) + (x²) / (4pi) = x


1x²/16 +x / (4pi) =x

je ne comprends pas ce que tu fais .
je reprends la somme des aires est y=(x/4)²+(1-x)²/(4)
soit y= x²/16 +(1-2x+x²)/(4)=(1/16).(x²+4+4x²-8x),
soit 16y=(+4)x²-8x+4
Cette expression a pour dérivée 2(+4)x-8 ,
et cette dérivée s'annule pour x=4/(+4)
Vérifie tout de même les calculs .
Et bonne nuit .
Rolands .

Et maintenant je dois faire le discriminant ?

Tu m'as l'air bien dépassé , math54190 .
La question qui t'est posée est :
On coupe une ficelle de 1m de longueur en 2 morceaux .
...soit x la longueur du 1er morceau , celui dont on va former un carré.
...le morceau dont on fera un cercle mesure 1-x .
SOMMES-NOUS OK JUSQUE LA ?
------------------------
LE CARRE :
Son périmètre est x ,
---> le côté de ce carré est x/4 , donc sa surface S₁ est (x/4)²=x²/16 .
LE CERCLE :
Son périmètre est 1-x ,
--->Son rayon est r=(1-x)/2,sa surface  S₂=r²=(1-x)²/4²=(1-x)²/4 .
SOMMES-NOUS OK JUSQUE LA ?
------------------------
On veut que la somme des aires soit Minimum :
La somme des aires est S=S₁+S₂=x²/16 +(1-x)²/4=[x²+4(1-x)²]16.
S=(x²+4-8x+4x²)/16=[(4+)x²-8x+4]/16:
Il s'agit d'une expression du 2ème d°,elle représente une parabole à minimum car le coefficient de son monome du 2ème d° est >0 .
S sera minimum si (4+)x²-8x+4 est minimum , c'est à dire si la dérivée de cette expression est nulle

soit 2(4+)x-8 =0 c.à.d. si (4+)x=4 ,
ou encore si x=4/(4+).
SOMMES-NOUS OK JUSQUE LA ?
SI oui ---> merci ,
si non ---> précise tes questions .
Je te souhaite un bon week end .
Roland .

Oui je suis ok mais je conclue comment ensuite alors ? il faut donner la réponse sous forme d'intervalle alors ?

Il faut répondre à la question qui t'est posée :
A q[uel endroit doit-on couper la ficelle ...
Si AB est le bout de ficelle , il faut la couper au point C, entre A et B ,C tel que AC= 4/(4+).

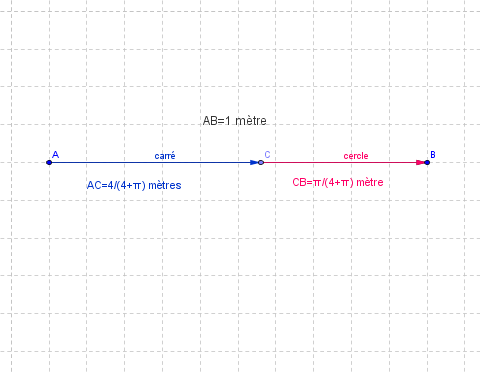
donc en gros il faut la couper a x=44+PI) et sa va me donner un résultat se serra ce que je cherche