Inscription / Connexion Nouveau Sujet
DM de mathématiques angles orientés
Bonjour
J'ai un DM à faire dont voici l'énoncé ci-après, et je sèche complètement.
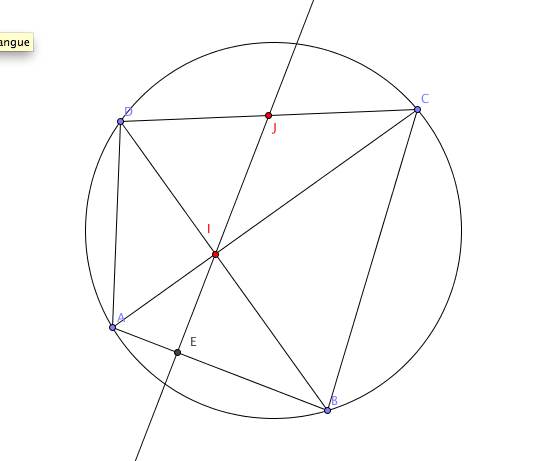
Dans le plan orienté (cf image ci-dessous), ABCD est un quadrilatère inscrit dans un cercle, quadrilatère dont les diagonales se coupent en I et vérifient () : π/2 (2π). Le point J est le milieu de [CD], et la droite (IJ) coupe (AB) en H.
Le but de ce problème est de démontrer que les droites (AB) et (IJ) sont perpendiculaires en évaluant l'angle orienté ().
On note 
une mesure de ()
1) Démontrer tout d'abord que () =
+ ().
2) On se propos ensuite d'exprimer une mesure de () en fonction de
. Pour cela :
a : Justifier la nature du triangle DIJ.
b : Exprimer une mesure de l'angle orienté () en fonction de
.
c : En déduire une mesure de l'angle orienté () en fonction de
.
3) Conclure en utilisant le résultat de la question 1.
Merci de m'aider, ça serait franchement super sympa, vous n'imaginez pas depuis combien de temps je patine dans la semoule à retourner le problème dans tous les sens.
Bonjour
parce que DIC est rectangle en I, donc demi rectangle dont J serait le centre, or les diagonales d'un rectangle ont même longueur...
Mais qu'est-ce que tu fais toi ? Tu attends qu'on te dise tout ? Point de vue connaissances cela ne dépasse guère le niveau de troisième, il y a juste l'orientation en plus.
Une conjecture effectuée grâce à GeoGebra me dit que DI, DC = mais je n'arrive pas à le démontrer. Est-ce que quelqu'un peut m'aider ?
Annuler
connectez vous