Inscription / Connexion Nouveau Sujet
DM de maths (2)
Bonjour. J'ai du mal pour cet exercice :/
Énoncé:
EXERCICE 2:
f(x) = -3x² -2x - 4 / 2x + 4
1. Déterminer l'ensemble de definition D de la fonction f.
2. Montrer que f est dérivable sur D et que pour tout x de D
f'(x) = -6x² - 24x / (2x+4)²
3. Dresser le tableau de variations de f sur D.
4. Peut-on trouver une ou des tangentes à L de coefficient directeur égal à 1.
5. Déterminer l'équation de la tangente au point d'abscisse -4.
J'ai donc fait:
u'(x)*v(x) - u(x)*v'(x) / v²
u(x) = -3x² - 2x - 4
v (x) = 2x + 4
u'(x) = - 3*3x² - 2*1 - 0
f'(x) = -3*3x² - 2*1 - 0 * 2x + 4 - (-3x²) - 2x - 4 * 2 * 1 + 0 / (2x + 4)²
f'(x) = -9x² - 6x - 2 - (-3x²) - 6x * 2 / (2x + 4)²
f'(x) = - 6x² - 24x / (2x + 4)²
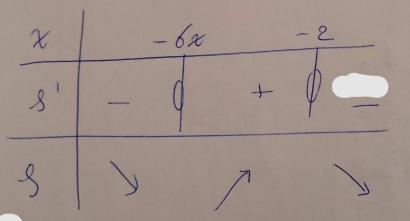
Tableau de variations: (screen)
Je ne comprends pas du tout le reste des questions. Serait-il possible de m'y m'éclairer ? Merci 
* Modération > Image recadrée, sur le tableau uniquement ! *
Bonjour
Les parenthèses sont indispensables
Question 1 non traitée
Question 2 d'où sort le 3 ?
les calculs sont peu explicites Que fait un en haut du tableau ?
Salut,
Ensemble de définition --> valeurs de x possibles pour calculer f(x)
Donc : y a-t-il une ou des valeurs interdites ?
J'ai fait:
2x + 4
f existe si 2x + 4 ≠ 0
On résout :
2x + 4 = 0
2x = - 4
Donc : x = - 2 ou x = 2 {-2;2}
Seul le dénominateur doit être non nul donc
d'où sort le +2 ?
u'(x) = - 3*3x² - 2*1 - 0
d'où
Le numérateur est toujours strictement négatif le dénominateur strictement positif donc
Merci beaucoup ! Mais du coup je suis toujours bloqué à mon tableau de signe... J'ai effectué une équation puisque je ne peux pas calculer delta vu que je n'ai pas d'équation du second degré:
-6x² - 24x que j'ai dérivé : -6*2x-24
2x = 6+24
2x = 30
30/2 = 15.
-6x² - 24x que j'ai dérivé : -6*2x-24
2x = 6+24
2x = 30
A quoi ça sert de dériver le numérateur de la dérivée ?
Comment "passes" -tu de -6*2x-24 à 2x = 6+24 ?
etc...
Et as-tu lu le message de hekla ? ...
Bonjour Yzz
Un seul être vous manque et tout est dépeuplé
Parce qu'il n'y a pas de alors ce n'est pas du second degré !!!
On ne connaît plus les facteurs la poste c'était mieux jadis
On vous demande un tableau de variation donc il faut le faire. Peut-être confondez-vous avec un tableau de signes qui ici était bien inutile.
J'ai compris. Sauf que je ne vois pas comment le faire sachant que je n'ai pas d'équation du second degré et donc que je ne peux pas calculer x1 et x2, donc bon...
est une équation du second degré où
et
. Il est inutile de chercher les solutions de l'équation il n'y en a pas
en effet et
est une somme de carrés dont l'un est strictement positif donc la somme est strictement positive donc JAMAIS nulle



