Inscription / Connexion Nouveau Sujet
DM de Maths : Exercice de Trigonométrie
Bonjour,
Voici mon exercice,
Dans le plan orienté, ABCD est un quadrilatère inscrit dans un cercle, dont les diagonales se coupent en I et vérifient ( ,
, ) =
) =  / 2 .
/ 2 .
J est le milieu de [CD] et (IJ) coupe (AB) en H.
Le but du problème est de prouver que (AB) et (IJ) sont perpendiculaires.
On pose ( ,
, ) =
) = 
PETITE PRECISION :
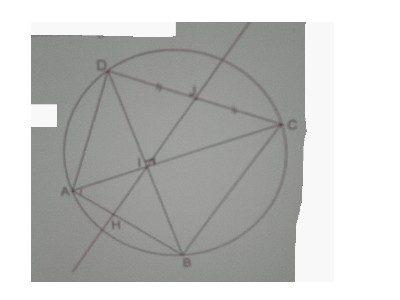
Je fais joindre ici, la figure qui correspond à l'énoncé
Donc en fait :  correspond au vecteur AC
correspond au vecteur AC
 correspond au vecteur BD
correspond au vecteur BD
 correspond au vecteur AB
correspond au vecteur AB
 correspond au vecteur IJ
correspond au vecteur IJ
 correspond au vecteur IC
correspond au vecteur IC
1. Prouver que ( ,
, ) =
) =  + (
+ ( ,
, )
)
Voila mon problème, si quelqu'un pourrait me montrer la démarche à suivre...
Merci
si c'est il doit y avoir une erreur dans ton enonce
la question se fait avec la relation de Chasles entre angles
et et comme
est un angle inscrit qui sous tend l'arc BC ( lu dans le sens trigo ) on le retrouve en
et donc en
car JDI est isocèle en J ... termine!
Donc je peux conclure que( ;
; ) =
) =  + (
+ ( ,
, ).
).
Mais j'ai une question, comment justifier que JDI est isocèle en J?
re
JDI est isocele en J car la mediane dans un triangle rectangle ICD est la moitie de l'hypotenuse IJ=JI=JC
Merci, J'ai encore une question
On me demande de déduire le (Vecteur IC, Vecteur IJ)en fonction de  ...
...
Comment doit-je M'y Prendre?
DIJ est isocèle en J et son angle en D c'est theta comme angle inscrit soustendant le meme arc BC que l'angle ( CAB)donc angle (DIJ)= theta et angle (ICJ )c'est son complementaire ( j'ai ecrit en angle style college pour faire plus simple c'est la mmeme chose en angles de vecteurs bien orientes sens trigo
erreur
angle (ICJ )c'est son complementaire ( j'ai ecrit en angle style college pour faire plus simple c'est la mmeme chose en angles de vecteurs bien orientes sens trigo
angle (CIJ )c'est son complementaire ( j'ai ecrit en angle style college pour faire plus simple c'est la mmeme chose en angles de vecteurs bien orientes sens trigo
Merci Beaucoup,
Maintenant je peux prouver que ( AB) et (IJ) sont perpendiculaires.
Mais comment je peux conclure?
tu as etabli :
dans le croquis j'ai passe les 3 segments egaux [ID] [IC] [IJ] ;en couleurs les 3 angles egaux à
en vert l'angle droit
Merci d'avoir répondu,
Mais le segment IC n'est pas égal aux autres segments, Je crois que c'est JC
Lorsque vous dites que (les vecteurs) (AB;IJ)= +(
+( /2 -
/2 - )+ k
)+ k
A quoi correspond le k de k ??
??
on peut peutetre mettre 2kpi , k est un entier
car d'autres figures ne permettent pas de savoir si les vecteurs colineaires sont de meme sens ou pas (i et v ),et les es angles sont tjrs definis à 2kpi pres
le quadrilatere pourrait etre croise
je ne voulais pas dire que IC=... c'est JC=JD=JI, un de mes petits traits de codage se voit mal

 (IJ)?
(IJ)? ?
?



