Inscription / Connexion Nouveau Sujet
DM de maths Fonction polynôme du second degré
Bonjour tout le monde, j'ai un DM de maths, et je bloque à partir de la question 2. Voici l'énoncé :
f est la fonction polynôme du second degré définie par f(x)=x²-4x+8. Cf est sa représentation graphique dans un repère orthonormal (O,vecteur i, vecteur j) du plan.
1/ Dresser le tableau de variations de f.
2/ Démontrer que pour tout réel a, f(a)=f(4-a). Que peut-on en déduire pour Cf ?
3/ Dessiner Cf.
4/ Démontrer la propriété : "0 est inférieur ou égale à x qui est inférieur ou égale à 4 équivaut à 4 est inférieur ou égale à f(x) qui est inférieur ou égale à 8."
5/ Résoudre dans R les équations suivantes et les interpréter graphiquement
a) f(x) = 2
b) f(x) = 4.41
c) f(x) = 4
Voilà, pour la deux j'ai réussi la première partie mais je ne vois pas ce que l'on peut en déduire pour Cf.
Pour la 3, je pense qu'il faut faire de tableau de valeur avec différente valeurs de x pour trouver différent points et tracer la courbe.
Pour la 4, aucune idée et pour la 5, il faut remplacer f(x) par la fonction (x²-4x-8) et mettre l'équation sur 0 puis calculer delta, mais pour interpréter ça graphiquement, je vois pas.
Merci en avance de votre aide !
Bonjour
À quoi correspond pour la courbe représentative de
la réponse à la question 3 facilitera peut-être l'interprétation graphique de 2
si je comprends bien
dans un sens utilisez le sens de variation de
5 quelle est la courbe d'équation
Bonjour, merci. Mais je ne vois pas ce que f(a) représente pour Cf, peut-être son coefficient directeur, je sais vraiment pas.
un point appartient à la courbe représentative de
si et seulement si ses coordonnées vérifient l'équation de la courbe
soient et
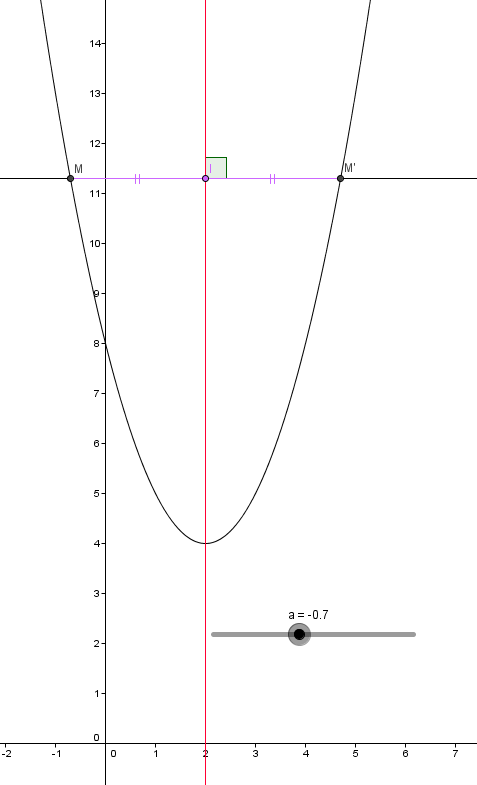
que pouvez-vous dire du milieu de
?
je vous avais demandé les coordonnées du milieu du segment [MM']
l'abscisse est quelque soit la valeur de
et l'ordonnée des deux points est la même
Que peut-on dire de la droite d'équation par rapport au segment [MM']?
Le milieu de MM' est (2;f(a)) donc la droite x=2 qui est parallèle à l'axe des ordonnés passe par [MM']. C'est ça ou pas du tout ?
deux points M et M' tels que soit la médiatrice de [MM'] sont symétriques par rapport à
est symétrique par rapport à la droite d'équation
N'avez-vous pas vu cela en seconde symétrie par rapport à ?
Non je n'ai pas le souvenir d'avoir vu ça, c'est peut-être pour ça que j'ai des difficulté sur cette question
Si x appartient à [0;2], f(x) appartient à [4;8]
Si x appartient à [2;4], f(x) appartient à [4;8]
Donc lorsque x est compris (ou égale) entre 0 et 4 ce la revient a dire que f(x) est compris (ou égale) entre 4 et 8, la propriété est donc démontré.
je sais pas si dans ce cas là c'est possible, mais j'ai fait la méthode de delta pour trouver les solution mais j'ai trouver un delta négatif et donc qu'une solution qui est 2.
première inéquation pas besoin de une petite factorisation suffit
résultat
quant à la seconde identité remarquable donc
intersection des 2 :
Ah d'accord, moi j'avais eu l'idée d'utiliser delta. Donc maintenant qu'est-ce qu'il me reste à faire ?
Pour quelle question ? pour la 4 c'est fini
on a montré que
on a montré que
il y a bien équivalence
reste la question 5
d'accord pour la 5, j'aimerai juste que vous m'aidiez pour l'interprétation graphique, il faut montrer quoi ?
Je dirais qu'après avoir trouvé les coordonnées de chacun des trois points, tu les places le repère ou tu as représenté Cf
je vous avais donné une indication
trouver les coordonnées des points d'intersection des deux courbes c'est résoudre le système
vous avez la première courbe
la seconde est une droite
lecture de l'abscisse des points d'intersection