Inscription / Connexion Nouveau Sujet
Dm derivation
Bonsoir a tous jai un dm a rendre pour demain et je bloque sur cet exercice
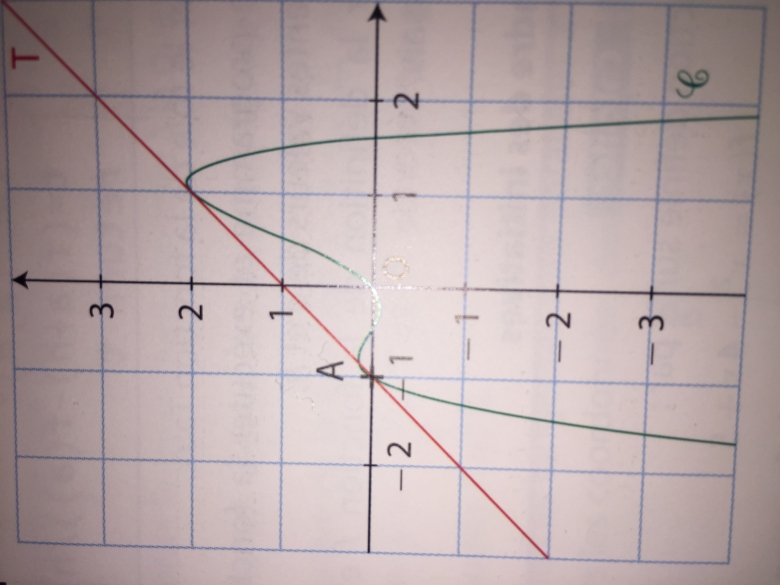
On nous demande de démontrer que la tangeante T a la courbe C au point A d'abscisse -1 est aussi tangeante a C en un autre point a préciser
Merci de votre réponse
sans la courbe, on ne peut pas t'aider.
Regarde dans la FAQ comment poster une photo (uniquement la figure, le texte doit etre tapé).
f(x)= -x^4 + 2x² + x ..
c'est ça ?
ton énoncé est complet ? il n'y avait aucune question avant ?
s'il y en a , tape les et montre ce que tu as fait..
Voici l'énoncé :
dans un repère orthonormé C est la courbe représentative de la fonction f définie sur R par FX = - x puissance 4 + 2 x au carré + x.
Démontrer que la tangente t à la courbe C au point a d'abscisse - 1 et aussi tangente à C en un autre point à préciser.
ok, donc pas d'autre question.
tu pourrais déjà calculer la dérivée, pour établir l'équation de cette tangente.
puis trouver les points communs entre ta courbe et cette droite...
f'(x)= ?
Donc je dois calculer la dérivée puis l'équation de la tangeante((f'(a)(x-a)-f(a))
Puis je trouve les points commun de cette équation avec la courbe?
ça c'est ce que je te propose..
c'est une façon de faire .
détermine déjà, la dérivée , puis l'équation de la tangente !
la derivée d'une constante et égale à 0, c'est vrai, mais là, on ne parle pas de ça..
tu as f'(x)= -4x^3 + 4x + 1
pour x=-1 ca donne f'(-1) = ??
voyons, Yasuu212,
on a déjà calculé la dérivée.. on a trouvé f'(x) = -4x^3 + 4x + 1
pour calculer f'(-1) tu remplaces x par -1 dans f'(x)..
dans -4x^3 + 4x + 1 si tu remplaces x par -1,
ca donne
-4(-1)^3 + 4(-1) + 1 = ?? je ne vois pas comment tu trouves 1*-4 ??
montre le détail de ton calcul
S'il vous plait aidez moi je n'y a arrive pas a comprendre
rassure toi, il n'y a rien à comprendre, il faut juste appliquer..
il faut que tu revoies le calcul littéral, les puissances, etc.... c'est important !
(-1)3 = -1 , ça n'est pas egal à 3
f'(-1) = -4(-1)^3 + 4(-1) + 1 = 4 -4 + 1 = 1
f'(-1) = 1 ca te donne le coefficient directeur de la tangente. (tu vois bien sur ta figure que ca ne peut pas etre égal à 4, 9, ou -4)..
à présent, s'il y a un autre point de la courbe qui admet la même tangente, c'est que, en ce point, la dérivée est aussi égale à 1..
tu es d'accord ?
on va donc poser -4x^3 + 4x + 1 = 1
on va résoudre, et on va voir si on trouve plusieurs solutions.
-4x^3 + 4x + 1 = 1
vas y !
Yasuu212, tu ne lis pas bien mes posts, je crois...
on va donc poser -4x^3 + 4x + 1 = 1
on va résoudre, et on va voir si on trouve plusieurs solutions.
-4x^3 + 4x + 1 = 1
vas y !
?? Yasuu212, tu fais autre chose en même temps ?
tu avais trouvé f'(x)= -12x + 4x + 1 pour ta dérivée ????
non, tu avais trouvé
f'(x) = -4 x^3 + 4x + 1
x^3 (x au cube, x3 ) ne vaut pas 3x... tu ne lis pas mes posts attentivement, je t'ai déjà signalé cette erreur juste avant..
alors à toi de résoudre
-4x3 + 4x + 1 = 1
vas y !
je suis désolée de le dire, mais tu écris n'importe quoi...
-4x3 + 4x + 1 = 1
-4x3 + 4x + 1 - 1 = 0
-4x3 + 4x = 0
je factorise par 4x
4 x ( -x² + 1) = 0
==> 4x (1-x² )= 0
quelles sont les solutions ?