Inscription / Connexion Nouveau Sujet
DM dérivé
Bonsoir,
Voici mon exo
Soit f la fonction définie sur I=[0;+[ par f(x)=x-sinx
a)Etudier les variations de f sur [0;+[.
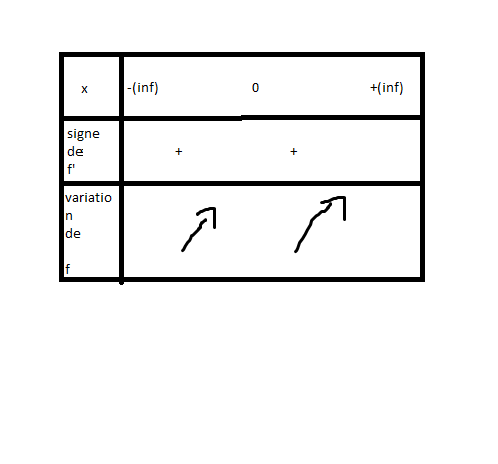
J'ai calculer la dérivée qui est f'(x)=1-cosx
Voilà ce que j'ai fait (voir tableau)
Est ce bien la façon dont il faut procéder ?
Est-ce juste ?
b) en déduire le signe de f sur I puis la comparaison de x et sinx.
f est donc positif lorsque x à I
par contre je ne comprend pas le reste de la question... comparer signe de x et de sinx ?
c)Soit g la fonction définie sur I par : g(x)=cosx-1+ x²/2
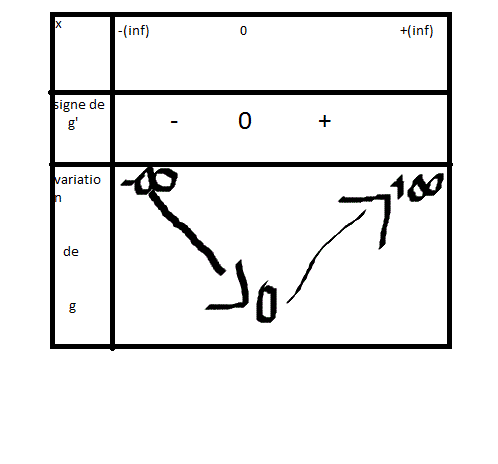
g'(x)= -sinx + 2x
_etudier les variations de g sur I
(suite)
Pour g(x)
-En déduire que pour tout x de I:
1-x²/2
cosx1
Je pense qu'il faut dire que cos x est compris entre -1 et 1 dans le cercle trigo.
Suis-je sur la bonne piste ?
Bonjour
C'est un bon début. a) est correct.
b) Comme f est positive pour x dans I, tu as x-sin(x)
0 donc sin(x)x ce qui servira dans la suite...
c) g'(x)=-sin(x)+x (et non 2x) Tu vois à quoi ça servait?
Est-ce que la fonction dérivée de cos(x)-1 + x²/2 est bien -sin(x)-x ?
*** message déplacé ***
* Océane > le multi-post n'est pas toléré sur le forum ! *
Annuler
connectez vous