Inscription / Connexion Nouveau Sujet
Dm dérivé
Bonjour, je suis en classe de première et j'ai un dm à faire. Cependant je bloque dans l'un des exercices:
Énoncer:
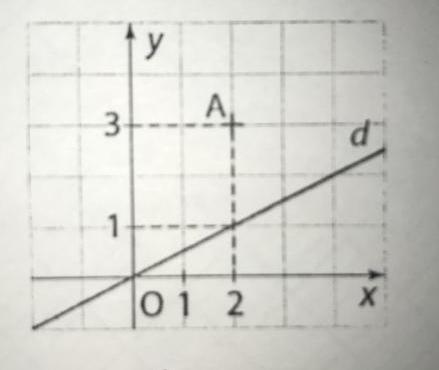
On considère la fonction trinôme f définie sur R par: f(x)=ax2+bc+c. C est sa courbe représentative. La droite d est tangente à C à l'origine du repère et C passe par le point A(2;3).
1) Démontrer que f(0)=0 puis que f'(0)=1/2 puis que f(2)=3.
j'ai fais:
f(0)=a(0)2+b*0+c
c=0, mais j'ai pas démontré que f(0)=0 la , si?
2) a) En déduire la valeur de c, de b et de a. Faut que j'attende d'avoir fini le 1)..
b) Qu'elle est l'expression de f(x)?
Je trouverais quand j'aurai à b et c.
bonjour
La droite d est tangente à C à l'origine
donc courbe comme tangente passent par l'origine donc....
allez, continue !
et n'oublie pas que si f(x)=ax2+bx+c (je suppose que tu as mal recopié là haut)
alors tu peux exprimer f'(x)
mais je ne vois pas le lien..
euh...ta question était
mais j'ai pas démontré que f(0)=0 la , si?
bonjour malou
c'est bizarre mais je n'avais vu aucun de vos post sur mon écran quand j'ai rédigé mon message
f(0)=ax2+bx+c=0
a*02+b*0+c=0
c=0
f'(0)=a*2x+b=1/2
a*2*0+b=1/2
b=1/2
f(2)=a*22+b*2+c=3 je remplace b et c:
4a+(1/2)*2+0=3
4a+1=3
4a=2
a=2/4
a=2
donc j'ai bien mes valeurs de c b et à pour la question 2)à. mais est ce que mes calcul démontre bien de f(0)=0, f'(0)=1/2 et f(2)=3 ?
et pour 2)b. f(x)=1/2x2+1/2x
oui; tu avais certainement fait une erreur d'inattention
1) Démontrer que f(0)=0
comme le point est sur la courbe et sur la tangente à la courbe , la courbe passe par l'origine et f(0)=0
question 2)à. mais est ce que mes calculs démontrent f'(0)=1/2 et f(2)=3 ? on ne te demande pas de démontrer; ce sont des données
et pour 2)b. f(x)=1/2x2+1/2x OK
pour f'(0)=1/2 tu peux le visualiser sur le graphique puisque c'est la pente de la tangente en x=1/2
par contre pour f(2) tu ne peux rien démontrer puisque tu ne connais pas l'équation de la courbe; tu peux juste dire que lorsque un point est sur une courbe , ses coordonnées vérifient l'équation de la courbe
C passe par le point A(2;3) signifie, ce que tu as très bien compris, que f(2)=3
Donc si je réécris tout:
1) f(x)=ax2+bx+c, donc
f'(x)=a*2x+b
f(0)=ax2+bx+c=0
a*02+b*0+c=0
c=0
f'(0)=a*2x+b=1/2
a*2*0+b=1/2
b=1/2
f(2)=a*22+b*2+c=3
4a+(1/2)*2+0=3
4a+1=3
4a=2
a=2/4
a=1/2
2) a. Donc a=1/2, b=1/2 et c=0
b. f(x)=(1/2)x2+(1/2)x



