Inscription / Connexion Nouveau Sujet
dm math suite
Bonjour, pouvez vous m'aider, je n'arrive surtout pas à démarrer aidez moi svp. Merci
On sait tous qu'il y a des années a coccinelles et d'autres sans !
On se propose d'´étudier l'´évolution d'une population de coccinelles a l'aide d'un modèle utilisant
la fonction numérique f définie par f(x) = kx(1 -x), k étant un paramètre qui dépend de
l'environnement (k appartenant à R).
Dans le modelée choisi, on admet que le nombre des coccinelles reste inférieur a un million.
L'effectif des coccinelles, exprime en millions d'individus, est approche pour l'année n par un nombre reel Un avec Un compris entre 0 et 1. Par exemple, si pour l'année zéro il y a 300 000
coccinelles, on prendra U0 = 0,3.
On admet que l'´évolution d'une année sur l'autre a la relation Un+1 = f(Un), f étant la fonction définie ci-dessus.
Le but de l'exercice est d'étudier le comportement de la suite (Un)pour différentes valeurs de
la population initiale U0 et du parametre k.
Question préliminaire :
Tracer le tableau de variation de f sur [0;1]
Question 1 : Graphique 1
k=1 et u0= 0.4
1) b) Quelles conjectures peut on émettre quand à la suite Un
2) a ) Déterminé un+1 en fonction du un
b) calculer un+1-un
en deduire le sens de variation de un
3. conjecturer graphiquement la limite de un
4 que peut on dire de l'évolution à long terme de la pop de cocinnelle.
Question 2 : Graphique 2
k=1.8 et u0=0.3
1b) quelles conjectures peut on émettre quand à la suite un
2. que peut on dire de l'évolution à long terme de la pop de cocinnelle.
Question 3 : Graphique 3
k=3.2 et u0= 0.8
formuler une conjecture sur l'évolution de la pop de cocinnelle.
merci

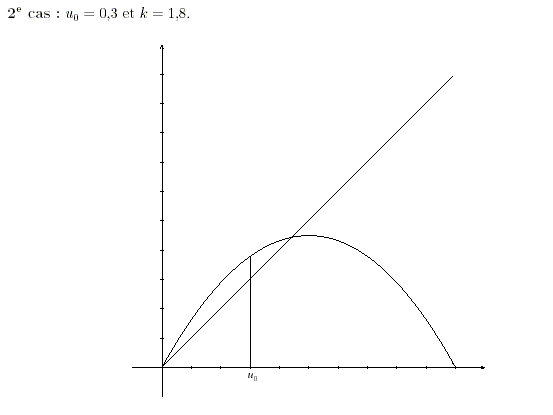
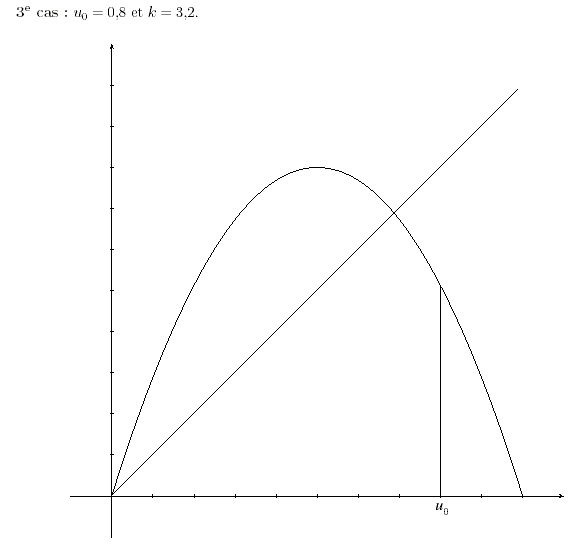
Déjà, il faut que tu connaisses le principe de la représentation graphique des suites récurrentes.
tu as la méthode expliquée là si tu veux ![]()
tu dessines la courbe (ici y=kx(1-x)) et la droite y=x qui sert à rabattre les points de l'axe des y sur l'axe des x pour pouvoir continuer la récurrence. Les segments semblent rebondir un coup sur la courbe et un coup sur la droite; A chaque verticale bleue, il y a un terme de la suite.
Et puis rien que pour te montrer que le comportement d'une suite, ça peut aussi être un peu chaotique, regarde ce que ça donne avec k = 4 et U0 = 0.8 :
quelle question tu dis ? et c'est le tableau de variation de la fonction ?
c'est une parabole tournée vers le bas, tu sais trouver le sommet et ses variations normalement.
oui tableau de variation j'ai trouve alpha = -b/2a c'est bon mais mtn je coince sur toute la question 1
1) b) Quelles conjectures peut on émettre quand à la suite Un
il te suffit de regarder le graphique
b) calculer un+1-un
tu as essayé de former un+1-un et de le simplifier ? son signe est vraiment simple à trouver.
je peux conjecturer qu'il s'agit d'une suite par récurrence La suite (u n ) est croissante, majorée par 1 donc est convergente,
La suite (u n ) est croissante
plutôt raté ! tu n'as pas bien dû regarder le dessin ni vraiment trouvé le signe de Un+1-Un

Soit n un entier naturel,
un+1 - un = un(1 - un ) - un = -u²n
pour tout n, u²n > 0 donc -u²n < 0 donc un est strictement décroissante cest sa?
mais Soit n un entier naturel,
un+1 - un = un(1 - un ) - un = -u²n
pour tout n, u²n > 0 donc -u²n < 0 donc un est strictement décroissante cest sa? c'est pour en deduire le sens de variation mais pour le calculer je fais comment?
pour la question calculer un+1-un
Soit n un entier naturel,
un+1 - un = un(1 - un ) - un = -u²n
pour tout n, u²n > 0 donc -u²n < 0 donc un est strictement décroissante cest sa?
je peux mettre sa
si Un+1-Un < 0 c'est que la fonction est décroissante comme tu l'as très bien dit. Donc tu l'as ton sens de variation.
tu as montré que c'était négatif donc que la suite était décroissante et c'est tout ce que l'on te demandait.
il me reste quelles conjectures peut on émettre quand a la suite un graphique 1
quelles conjectures peut on émettre quand a la suite un graphique 12
Et bien regarde les dessins que je t'ai fait.
quand a la suite un graphique 12
 c'est quoi un graphique 12 ?
c'est quoi un graphique 12 ?tu ne vois pas comment évoluent les termes de la suite dans les différents dessins ?
on voit bien pourtant si la suite croît ou pas , et vers quoi ça converge (quand ça converge).
ou alors c'est que tu n'as rien compris aux dessins ?
1)b) Je peux conjetcurer que la suite Un est décroissante et quelle converge vers 0
1b) graph 2 : Je peux conjecturer que la est croissante et converge vers 0.43 ?


