Inscription / Connexion Nouveau Sujet
DM maths : étude fonction
bonjour, j?ai un DM à faire mais je me bloque au première exercice vous pouvez m?aider svp.. 
On note f une fonction définie sur [......;......] et Cf sa représentation graphique dans le repère ci-dessous ( image ).
1)a - Déterminer graphiquement l?image de 5 et de -2 par f :
b - Déterminer graphiquement les antécédents de 0 par f :
c - Déterminer si les points suivants appartiennent à la courbe Cf : M(0;1) et P(-5;0) . Placer ces points sur la figure.
d - Résoudre graphiquement f(x) =3
puis f(x) ?1.
e- Dresser le tableau de variations de f :
f- Dresser le tableau de signes de f(x) :
g- Lire graphiquement le maximum de f et la valeur qui permet de l?atteindre.
h- Donner un encadrement de f(x) sur l?intervalle [2;6].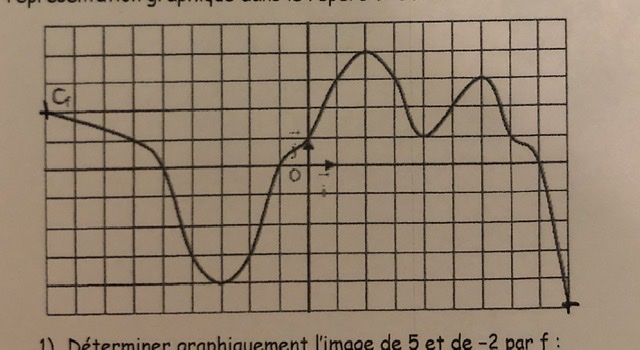
***Titre complété***
Bonsoir
intervalle de définition vous comptez les carreaux à gauche de 0 ce sera négatif à droite positif
les crochets fermés puisque c'est ce que l'on vous dit
Qu'est-ce qui vous gêne pour lire l'image de 5 ?
Vous avez bien vu des fonctions en seconde
un carreau représente une unité à gauche 9
lecture de l'image de 5 on repère 5 sur l'axe des abscisses on lit l'ordonnée du point d'intersection de la droite parallèle à l'axe des ordonnées avec la courbe
apparemment donc
antécédents de 0 : on lit les abscisses des points d'intersection de la courbe avec la droite parallèle à l'axe des abscisses autrement appelé axe des abscisses
placez les points sont-ils sur la courbe ?
Je tiens à préciser que j'ai des difficultés de compréhension en maths. Nous avons vu le chapitre certe en seconde mais j'ai beaucoup de difficulté en maths donc je ne m'en souviens pas beaucoup.
Bien sûr
pour les antécédents de 0 je vous avais dit comment les lire
abscisse des points d'intersection de la courbe avec l'axe des abscisses
il y en a trois le premier est
Les antécédents de 3 sont 1, 3 et 6
ou l'ensemble solution de l'équation est
donc c'est bien
Les deux écritures pour vous montrer que les deux formulations ont la même signification
Pour résoudre on trace la droite d'équation
et
on lit les abscisses des points pour lesquelles la courbe est située en dessous ou sur cette droite
Il me semble que le maximum est plutôt 4 pour
il me semble que varie plutôt de 1 à 4
Comment pouvez vous dire en g que le maximum est 3 et en h 5 ?
Donc pour la g) c'est F admet en maximum 4 pour x
et la h) c'est « Sur l'intervalle [2;6] on a 1<f(x)<4 » ?



