Inscription / Connexion Nouveau Sujet
DM maths géométrie,fonctions...
Bonsoir j'ai un dm à faire,
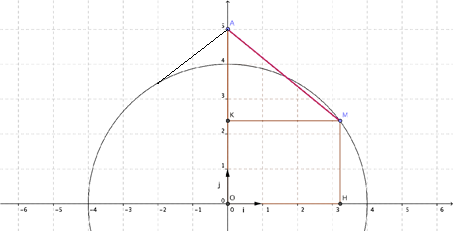
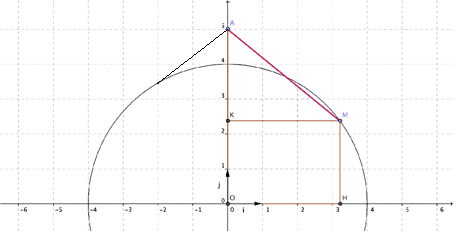
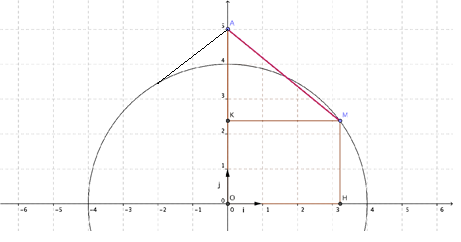
Dans le plan muni d'un repère orthonormé (O, i , j ) , on considère le demi-cercle C de centre O et de rayon 4 unités. On considère le point A (O;5) et le point M du demi-cercle C d'abscisse x. Les points H et K sont les projetés orthogonaux du point M sur l'axe des abscisses et l'axe des ordonnées, conformément à la figure ci-dessous.
1. On considère la fonction f définie par : f(x) = AM. Donner la domaine de définition de la fonction f.
2. Placer sur la figure ci-dessus le point M du demi-cercle C d'abscisse -2. Tracer le segment [AM] correspondant.
Conjecturer les variations de la fonction f sur son domaine de définition.
3. Exprimer OK puis AK en fonction de x.
4. On considère la fonction u définie par u(x) = AM2
Démontrer que u (x) = 41 - 10 16 - x2
16 - x2
5. Déterminer, en justifiant rigoureusement par les propriétés vues en cours, les variations de la fonction u sur l'intervalle [0;4] puis sur [-4;0]
6. Déterminer, en justifiant rigoureusement, les variations de la fonction f sur son domaine de définition. Dresser son tableau de variations. Préciser les éventuels minimum et maximum.
7. On considère maintenant l'aire du quadrilatère AMHO. Préciser la nature du quadrilatère. Exprimer son aire g(x) en fonction de x.
8. Compléter le tableau de valeurs ci-dessous :
| x | 0 | 0,5 | 1 | 1,5 | 2,0 | 2,5 | 3 | 3,5 | 4,5 |
| g(x) |
En déduire un encadrement d'amplitude 1 de la valeur qui réalise ce maximum de la fonction g.
9. Réaliser un autre tableau de valeurs qui permette de donner un encadrement d'amplitude 0,1 de la valeur qui réalise ce maximum.
10. Déterminer avec le logiciel XCAS la valeur exacte du maximum et la valeur exacte de la valeur qui réalise ce maximum.
J'espère que j'aurai tout fini avant la fin de la soirée avec de l'aide s'il vous plaît..
1) J'ai dit f = [0;4] ??? ou x a la place de 4
Bon voulais - je aller plus loin.
Quand on te demande le domaine, c'est dans le cas présent donner l'intervalle des valeurs de x
oui c'est ce que je voulais dire tout a fait le point M varie sur le demi cercle donc x compris entre -4 et 4
Tout de suite, je travaille avec une tablette. Donc impossible pour moi de t'envoyer un graphique.
Mais ton M sur le graphique de ton post de 21h07 n'a pas pour abscisse -2
ah non désolé ca le M initial tu n'as pas du bien comprendre alors , J'ai pas écris le M c'est peut etre ma faute, c'est la droite noire.
Pour la conjecture, en faite M c'est un point qui se déplace sur le demi-cercle si j'ai bien compris, donc lorsque M est sur [-4;0] la fonction f est décroissante et sur [0;4] f est croissante
Bon, dans la deuxième question, il est demandé de placer le point M d'abscisse -2.
Puis de conjecturer...
Si l'abscisse de M appartient à [-4;0], le coefficient de l'équation de la droite (MA) est bien positif. Non ?
je suis d'accord mais Imagions un point M à -4, et un autre point M à -1
On voit que la distance AM a racourci en passant de -4 à -1 ?
et de 0 à 4 la distance AM s'élargit...
mais c'est bizarre parce que je suis persuadé que j'ai raison 
f(x) : AM
au début du trajet partant de -4 à 0
AM diminue jusqu'à 0 ou il est égale à 1 d'après le graphique
donc f(x) est décroissant sur [-4 ;0]
AM augmente de 0 à 4 donc f(x) est croissant sur [0;4]
Ca me parait logique... ???
3) D'après le pythagore on a :
OM2 = OK2 + KM2
OM2 = OK2 + x2
42 = OK2 + x2
16 - x2 = OK2
OK =  16-x2
16-x2
?
Bon c'est pas grave, j'espère demain nous aurons le temps de finir
bonne nuit sur ce et bonne année.
bonjour,
Hier, j'étais quelque peu fatigué. Réveillon oblige!
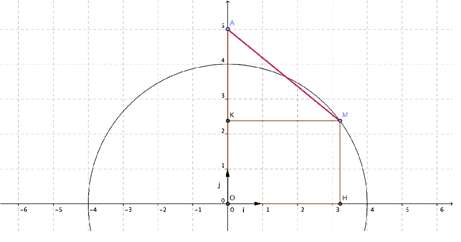
2. Placer sur la figure ci-dessus le point M du demi-cercle C d'abscisse -2. Tracer le segment [AM] correspondant.
Conjecturer les variations de la fonction f sur son domaine de définition.
f est décroissante sur [-4;0] (cela correspond à la diminution de la longueur AM sur la partie gauche du demi-cercle)
f est croissante sur [0;4] (cela correspond à l'augmentation de la longueur AM sur la partie droite du demi-cercle).
Salut,
J'ai résolu hier les 4 premières questions sans problème. C'était assez simple.
Pour AM je trouve également 41 -10 16-x2
16-x2
Peux-tu s'il te plaît restez avec moi pendant 1h30 environ, afin de finir rapidement ce dm s'il te plait si ca ne te dérange pas. J'essayerai d'etre plus efficace et rapide en te répondant
Si j'ai bien compris pour u(x) : il y a d'abord à calculer différentes fonctions :
16- x2
 16-x2
16-x2
-10 16-x2
16-x2
et enfin 41 - 10 16-x2
16-x2
??
Voici les 3 propriétés qu'on ait vu en cours en lien avec ici :
1ere : Soient f une fonction définie sur un intervalle I et k un nombre réel.
Les fonctions f et f+k ont les mêmes variations sur I
2eme Soient f une fonction définie sur un intervalle I et  un nombre réel.
un nombre réel.
Si  supérieur à 0, alors les fonctions f et
supérieur à 0, alors les fonctions f et  f ont les mêmes variations sur I
f ont les mêmes variations sur I
SI  inférieur à 0, alors les fonctions f et
inférieur à 0, alors les fonctions f et  f ont des variations contraires sur I
f ont des variations contraires sur I
3eme : Soit f une fonction définie sur un intervalle I, telle que pour tout x  I, f(x)
I, f(x) O
O
La fonction x
 f(x), notée
f(x), notée  f, a les mêmes variations sur I que f
f, a les mêmes variations sur I que f
bon finalement j'ai résolu tout seul la question 5)
après plusieurs calculs :
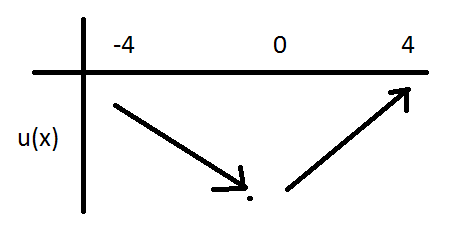
e(x) : 16 -x2 est croissante sur -4;0 et décroissante sur 0;4
h(x):  16-x2 d'après la 3eme propriété elle croissante sur -4;0 et décroissante sur 0;4
16-x2 d'après la 3eme propriété elle croissante sur -4;0 et décroissante sur 0;4
k(x) : -10 16-x2 d'après la 2eme propriété elle est décroissante sur -4; 0 et croissante sur 0;4
16-x2 d'après la 2eme propriété elle est décroissante sur -4; 0 et croissante sur 0;4
u(x) 41-10 16-x2 a les memes variations que k(x) d'après la 1ere propriété. donc u(x) :
16-x2 a les memes variations que k(x) d'après la 1ere propriété. donc u(x) :
6) f(x) = AM
u(x) = AM2
donc f(x) =  u(x)
u(x)
donc f(x) = AM2
AM2
=  41-10
41-10 16-x2
16-x2
d'après la 3eme propriété  u(x) et u(x) ont les mêmes variations donc f(x) a les mêmes variations que u(x)
u(x) et u(x) ont les mêmes variations donc f(x) a les mêmes variations que u(x)
Pour les minimum et maximum quelqu'un peut-il m'aider s'il vous plait ??? kenavo es-tu ici j'ai besoin de ton aide ?
Bon j'ai résolu enfaite
les maximum et minimum sont - 4, 0 et 4
donc f(-4) :  41
41
f(0) :  1 : 1
1 : 1
f(4) :  41
41
alors la 7)...
Bonjour
J'ai une question à vous poser
Je possède le logiciel XCAS, dans mon dm il est demandé pour g(x) = x*  16-x2 + 5*x /2 de trouver la valeur exacte du maximum et la valeur exacte de la valeur qui réalise ce maximum dans l'intervalle (0;4)
16-x2 + 5*x /2 de trouver la valeur exacte du maximum et la valeur exacte de la valeur qui réalise ce maximum dans l'intervalle (0;4)
sachant que g(x) calcule l'aire du trapèze AMHO.
je ne sais pas utiliser du tout XCAS si vous pouviez m'aider s'il vous plait merci
*** message déplacé ***
g(x) calcule l'aire du trapèze rectangle AMHO.
Il faut trouver l'aire maximum pour quelle valeur avec exactitude via XCAS dans l'intervalle [0;4].
Dans le schéma le point M se déplace sur le demi cercle...
*** message déplacé ***
Ca serait vraiment sympa que quelq'un vienne me dépanner j'atend une réponse depuis 30 mins...
*** message déplacé ***
Bonjour,
j'attend une réponse depuis 30 mins...
sur un forum ce n'est pas un chat de discussion instantanée, calme toi !!!
une solution avec Xcas est de lui demander de calculer la dérivée de cette fonction par diff() et de résoudre g'(x) = 0 par solve()
il faut de toute façon pour apprendre à utiliser Xcas chercher soi-même dans l'aide
l'habitude d'y rechercher étant indispensable à une bonne pratique de ce logiciel.
(et pendant 30 minutes tu n'as pas eu l'idée de chercher dans l'aide ou dans les exemples ???)
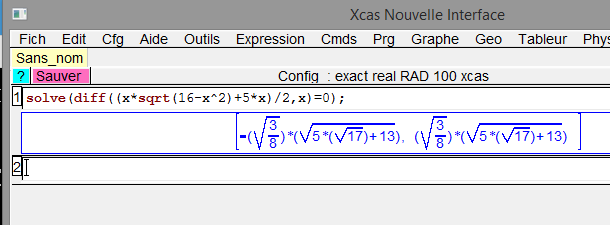
on peut tout faire en une seule ligne :
solve(diff((x*sqrt(16-x^2)+5*x)/2,x)=0);
et il donne les valeurs de x pour lesquelles il y a un extrêmum
après c'est l'étude théorique qui donnera les variations
(on peut toujours lui faire tracer la courbe aussi, n'est ce pas ... idem : lire l'aide)
*** message déplacé ***
tout d'abord merci d'être venu a mon secours
si si ne vous inquiétez pas je cherchai.
cependant je viens d'essayer votre technique :
le logiciel se ferme tout seul
*** message déplacé ***
exact je trouve pareil mais est-ce dans l'intervalle [0;4] ??
en faite moi dans l'intervalle j'ai fait un tableau d'abord, j'ai vu que pour x compris entre 3 et 4 g(x) =12.14 envirion
puis j'ai fait a l'échelle 0.1 donc:
*** message déplacé ***

 x
x