Inscription / Connexion Nouveau Sujet
DM - Nombre d'or et rectangle d'or
(le titre "Nombre d'or et rectangle d'or" est celui de l'exercice)
Bonjour à tous et merci à ceux qui vont lire et encore plus à ceux qui vont me répondre, c'est pour demain, je m'y suis pris trop tard mais on est pas là pour débattre de ça, voici l'énoncé et les différentes questions :
----------------------------------
Dans cet exercice, on prend 5 cm comme unité de longuer.
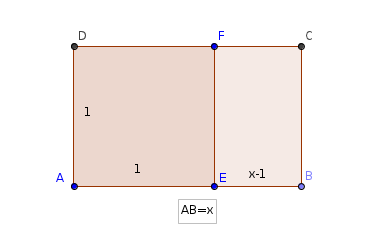
Soit ABCD est un rectangle de longueur AB = x avec 1 < x < 2 et de largeur AD = 1
Soit E sur [AB] et F sur [CD] tels que AEFD soit un carré.
Faire une figure.
On appelle [i]format[/i] d'un rectangle, le quotient L/l de la longueur par la largeur de ce rectangle.
1. Exprimer, en fonction de x, les formats de chacun des rectangles ABCD et EBCF.
2. Quelle relation doit vérifier x pour que ABCD et EBCF aient le même format ? Montrer que x vérifie alors l'équation x²-x-1=0.
3.
a) Résoudre dans R l'équation x²-x-1=0.
b) On désigne par a la solution psitive. Déterminer la valeur exacte de a, puis la valeur approchée arrondie à 10-2.
Dans ce cas, on dit que ABCD est un rectangle d'or.
--------------------------------
Voilà donc l'énoncé, en dessous de l'exercice il est rajouté :
"Un peu d'histoire" :
-¤ = 1+V5/2 est le nombre d'or
- blablabla ( histoire sur les bâtisseurs de cathédrales hors sujet )
J'ai retiré l'info : 0.2¤ = 0.3236.
J'ai utilisé ¤ pour schématisé le signe du nombre d'or qui est impossible à faire / trouver sur mon clavier.
Voilà toutes les infos que j'ai sur l'exercice.
J'ai commencé à chercher un peu, j'ai trouvé plusieurs égalités logiques, mais sans conclusion, j'ai regardé un peu sur internet, j'ai trouvé à peu près certaines cohérences mais pas de quoi écrire concrètement des réponses.
Par exemple je n'ai pas très bien compris le "on prend 5cm pour référence"
5cm = 1 ?
donc par exemple le AD = 1 est en fait AD = 5cm sur la figure ?
Et le 1 < x < 2 c'est 5cm < x < 10cm ??
Un peu confus pour moi, quelques calculs comme ça sur ma calculette :
On a fait un programme pour trouver Delta et les solutions qui s'en suivent à partir d'une équation du second degré qui est égal à 0.
J'ai donc pris le x²-x-1=0, j'ai trouvé Delta = 5 ( comme la référence, 1ere coïncidence)
première solution positive : 1.61 environ
deuxième solution négative je sais plus mais je sais qu'elle est mauvaise et incohérente.
Pour vérifier, j'ai fais 1.61²-1.61-1 et ça m'a donné 5.
C'est juste, oui, ça peut m'aider oui, mais comment ? je sais pas, et à quelle question et quand ? J'en sais rien non plus...
J'ai fais un brouillon non concluent avec des incohérences, et au final je tourne en rond, car il dit de faire un rectangle avec ABCD et sur tout ce que j'ai pu voir sur internet, ABCD est un carré et le rectangle c'est autre chose, j'ai vu comment le faire mais il dit pas vraiment pareil dans cet énoncé j'ai l'impression, au final je suis complètement perdu ^^ Si vous avez pas compris quelque chose ou si vous voulez me demander quelque chose j'essayerai de guetter un peu l'avancée du post^^
Encore merci.
Cordialement
merci, par contre pour la question 2 et 3, tu n'aurais pas un exemple de rédaction ? étapes de calculs et phrases de conclusion ?
Pour la 1 je sais quoi faire, mais pour la 2 je vois pas trop d'où sort le (x-1) et les étapes jusqu'à donc x²-x-1=0 :s
Pour la 3, les réponses ne collent pas à
a) Résoudre dans R l'équation x²-x-1=0.
b) On désigne par a la solution psitive. Déterminer la valeur exacte de a, puis la valeur approchée arrondie à 10-2.
Quelques explications ? ^^'
1. Exprimer, en fonction de x, les formats de chacun des rectangles ABCD et EBCF.
2. Quelle relation doit vérifier x pour que ABCD et EBCF aient le même format ? Montrer que x vérifie alors l'équation x²-x-1=0.
x(x-1)=1
x²-x-1=0
3.
a) Résoudre dans R l'équation x²-x-1=0.
b) On désigne par a la solution positive. Déterminer la valeur exacte de a, puis la valeur approchée arrondie à
Forme canonique
Identité remarquable
Solutions
or donc
généralement, on attribue plutôt la lettre phi au nombre d'or
Pour la valeur approchée, aucune méthode n'étant imposée, il suffit de savoir se servir d'une calculatrice
à la précision demandée, cela nous donne
Encore un grand merci dhalte !
Je me permet juste de te demander une dernière faveur pour la question 3, la réponse bien complète que tu m'as donnée, je vais retirer les indications au dessus des étapes "Forme canonique, identité remarquable etc" et donner directement 1,62 ; par contre il y a la question a et la question b et il faudrait que je sépare les deux.
Et dans ta démarche je ne vois pas trop ou s'arrête la question a et où commence la b...
Et la dernière chose, ceci : or 1 <  5 donc x1 < 0
5 donc x1 < 0
il me semble que c'est 1 < x < 2 et non pas 1 <  5 donc x1 < 0
5 donc x1 < 0
Désolé de mon incompréhension, je comprends pas tout sur ce coup...
ton énoncé t'indique 1<x<2, ce qui permet de limiter le problème (x<2) et de faire que AB soit bien la longueur du rectangle ABCD (puisque AD=BC=1 < x)
mais cette condition n'interdit pas d'utiliser d'autres données que l'énoncé ne rappelle pas (car elles doivent être connues), en particulier, j'utilise pour prouver que
donc n'est pas la solution cherchée, puisqu'on veut la solution positive (encore une indication de l'énoncé)
quant à séparer a) et b), tu ne comprends pas quel mot exactement ?
Ce n'est pas un mot en particulier que je ne comprends pas, c'est toujours la même chose :s
"ton énoncé t'indique 1<x<2, ce qui permet de limiter le problème (x<2) et de faire que AB soit bien la longueur du rectangle ABCD (puisque AD=BC=1 < x)
mais cette condition n'interdit pas d'utiliser d'autres données que l'énoncé ne rappelle pas (car elles doivent être connues), en particulier, j'utilise 1<sqrt5 pour prouver que x_1<0 donc n'est pas la solution cherchée, puisqu'on veut la solution positive (encore une indication de l'énoncé) "
Sur tout ce que tu as écris là j'ai pas trop compris la démarche, il me semble pas l'avoir déjà vu en cours en faites.
Ce qui m'aiderait c'est d'avoir par exemple :
a) Les étapes de calcul sous forme canonique :
- ........
- ........
- ........
etc
Sans de liaisons spéciales entre elles, et à la fin une phrase pour donner la réponse en lettre.
Pareil pour le b) :
b) Toutes les étapes de calculs en forme canonique et à la fin une phrase du genre
La valeur approchée au blablabla est 1,62 ...
C'est ça pour moi séparé^^
Dans ce que tu as écris plus haut pour le 3) a) et b)
Remettre une premiere partie dans le a, et la suite dans le b) et pas tout d'un coup.
attends, je te rédige un mode d'emploi détaillé (il va faire au moins 150 pages, alors il me faut un peu de temps)
C'est pas pour vexer ni pour être exigent ni pour quoi que ce soit :s
C'est le "1<sqrt5 pour prouver que x_1<0" : sqrt c'est quoi ? et pourquoi il y a un 0 ?
Sinon vu que tu m'as demandé ce que c'est séparé je t'ai expliqué le plus possible... Je peux pas tout rédigé d'un coup dans le 3, il faut que je mette un trucs dans le a puis dans le b, et dans tes étapes de calculs je ne vois pas où est la réponse du a parce que je n'ai pas compris la question, le "R" je ne sais pas ce que c'est.
Bref, merci en tout cas...
je t'incite à comprendre au moins ce que je t'ai écrit
par exemple j'ai écrit
or donc
tu as réécris
or 1 <  5 donc x1 < 0
5 donc x1 < 0
par la suite, je reprends le même argument, mais il est mal retranscrit
or donc
et tu me demandes ce qu'est sqrt !
allez, je réessaie, mais si tu fais l'effort de poser des questions, tu ne fais en revanche aucun effort digne d'être noté positif
or nous savons que , donc
donc
donc
je te reproche de ne pas avoir, à partir de l'affirmation
or
su établir les deux étapes intermédiaires qui amènent à
donc
Je ne serai pas assis à coté de toi lors de tes examens...
Là j'ai compris... Merci de t'inquiéter pour moi mais faut pas 
En relisant bien et avec ton dernier message, j'ai réussi à comprendre ce que je devrais écrire ! Merci !
J'ai le raisonnement, il faudra à présent que je retranscrive tout et que je mette nombre d'étapes entre chaque ligne mais c'est pas grave.
Par contre une dernière chose, je cerne pas trop ça :
a) Résoudre dans R l'équation x²-x-1=0.
b) On désigne par a la solution positive. Déterminer la valeur exacte de a, puis la valeur approchée arrondie à 10-2.
Dans ce cas, on dit que ABCD est un rectangle d'or.
Je sais quoi écrire dans le 3 si il y avait qu'une question, mais les deux décomposées, je sais pas.
Est-ce que ce serait a) Jusqu'à x1 et x2 ( les solutions )
Et au b) je choisis la solution positive, et je donne la valeur exacte et approchée.
Il me semble que c'est ça finalement




