Inscription / Connexion Nouveau Sujet
DM pentagone sur cercle trigonométrique
Partie A
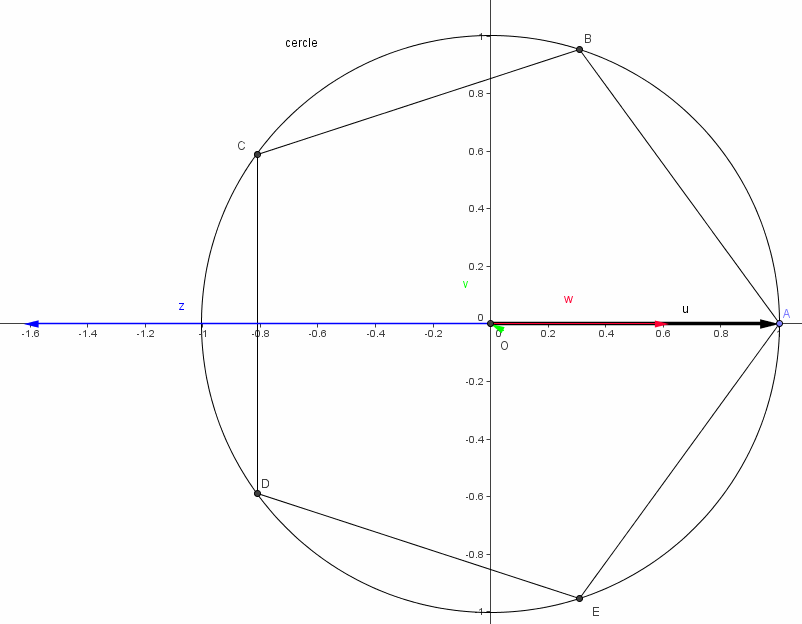
1)Créer le cercle C trigonométrique appeler O le centre.
2)Créer le point A(1;0)
3)Créer le point B sur le cercle C tel que (,
)= 2
/5 rad.
4)Créer le polygone régulier ABCDE inscrit dans C.
5)Créer les vecteurs 
=,
=+
,
=
+
.
Quelle conjecture peut-on émettre sur les vecteurs et ? sur et ?
6)Créer le vecteur 
=+
+
+
+
Partie B
1) Justifier que (,
)= 2
/5, (,
)= 4
/5, (,
)= 6
/5, (,
)= 8
/5.
2)En déduire les coordonnées de A, B, C, D et E puis celle de =+
+
+
+
3)Démontrer votre conjecture émise à la question A5) et démontrer que est colinéaire à .
4)Montrer de même que est colinéaire à , à
, à
, et à
.
5) a) En déduire une démonstration à la conjecture émise au A6)
b) En déduire que 1 + cos(2/5) + 2cos(4/5) = 0
6) a) On admet que cos(2a) = 2(cos a)² - 1. En déduire que cos(2/5) est solution de l'équation 4x² + 2x - 1 = 0
b) Déterminer alors la valeur exacte de cos(2/5)
Désolé j'ai oublié de vous demander si vous pouviez m'aidez ( si possible ^^ ), car je bloque à certaine questions mais j'ai réussi à répondre à certaines questions :
Partie A
3) Les vecteurs et sont de même direction et de même sens.
Les vecteurs et sont de même direction et de sens opposés
4) le vecteur est nul.
Partie B
1)1) On sait que ABCDE est un pentagone régulier . Or Ds un pentagone régulier , les pts ABCDE sont équidistant du centre de ce polygone et il a 5 cotés égaux.
Donc les angles du pentagone en partant du centre seront égaux à 360/5 = 72° = 2pi/5
Donc ( OA ; OB )= 2pi/5
(OA ; OB ) + ( OB ; OC) = 2pi/5 + 2pi/5 = 4pi/5 = ( OA ; OC) ( ce sont tous des vecteurs )
Bonjour quand même...
Quelles sont tes propositions de réponse ?
A la question 5b tu as oublié un coefficient 2 :
5 - b) En déduire que 1 + 2cos(2
/5) + 2cos(4/5) = 0
Je n'avais pas vu ton message de 19 h 50 en répondant.
D'accord avec tes réponses, tu peux même ajouter le mot "colinéaires" pour les réponses en A - 3 :
3) Les vecteurs
Les vecteurs
Vraiment désolé mais j'ai aussi oublé de dire que ABCDE est un pentagone régulier inscrit dans le cercle si jamais ca peut aider...
ouhlala tu as raison j'ai oublié le cofficient 2 a la question 5b
Je suis vraiment tête en l'air
Ah oui et Bonjour , vraiment je suis tête en l'air c'est pas possible...
Alors j'ai réussi les questions 1 et 2 de la partie B mais alors la question 3 je bloque complétement 
salut à tous !
Alors voila, j'aurais besoin de votre aide pour la partie B de ce dm ? Je ne comprends pas comment il faut faire pour demontrer que le vecteur V est colinéaire au vecteur OA de meme pour les vecteurs U ,v, et w
D"après ce que j'ai vu , il faut regarder les coordonnées de V mais je ne vois pas comment faut faire !
PS: est ce que vous pouvez m'expliquer comment faut faire SVP
merci d'avance !
bonne soirée a tous !!
Annuler
connectez vous