Inscription / Connexion Nouveau Sujet
DM produit scalaire, vecteurs
Bonjour, j'ai ce DM à faire et je n'arrive pas à décoller.. Si quelqu'un de vous pouvez prendre un peu de son temps pour m'aider..
Dans un repère orthonormé (O, i, j), on considère les points A(4;6), B (1;-2) et C (19;2)
1)déterminer les coordonnées des milieux I,J,K respectivement des segments [AB],[BC] et [CA].
2)déterminer une équation des médiane (AJ) et (CI)
3)en déduire les coordonnées du centre de gravité G
4)déterminer une équation des médiatrices de [AB] et de [BC]
5)en déduire les coordonnées du point 0, centre du cercle circonscrit au triangle ABC
6)déterminer une équation des hauteurs issues de A et de C
7)en déduire les coordonnées de l'orthocentre H
8) déterminer les coordonnées des vecteurs OG et OH
9)en déduire que O,G et H sont alignés ( cette droite est appelée la droite d'Euler )
Cordialement.
Lou.
Oui j'ai fait le 1) :
I milieu de AB
xi= xa+xb / 2 = 4+1 /2= 2.5
yi= ya+yb / 2 =6+(-2)/2 =2
J milieu de BC
xj=xb+xc / 2 =1+19 /2=10
yj=yb+yc / 2 =-2+2 /2= 0
K milieu de CA
xk=xc+xa /2 =19+4 /2=11.5
yk=yc+ya /2 =2+6 /2 = 4
d'où I (2.5 ; 2), J (10 ; 0) et K (11.5 ; 4)
Voilà
2) applique la méthode pour trouver l'équation d'une droite passant par deux points.
Calcul du coefficient directeur; puis ensuite détermine la valeur de b (équation de la forme y=ax+b) en écrivant que les coordonnées d'un des deux points vérifient l'équation de la droite.
certes...
tu dis que la droite (AJ) a une équation de la forme y = mx +p avec m=(yJ-yA)/(xJ-xA) et que l'on a
yJ = (yJ-yA)/(xJ-xA) * xJ + p et tu en deduis p.
tu fais la meme chose pour (CI)
je te mets une figure avec toutes les droites et points afin que tu puisses vérifier tes résultats de calculs à venir
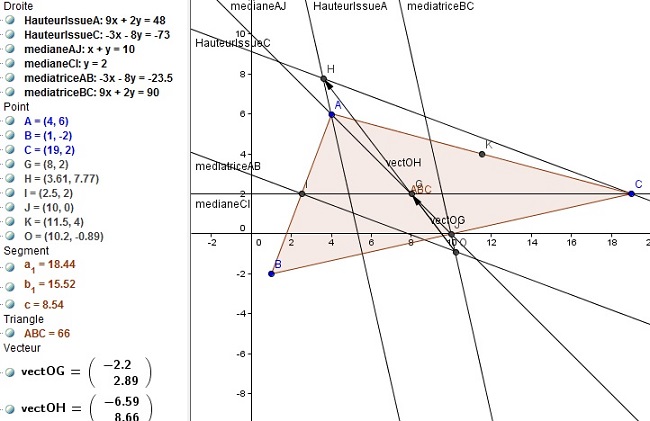
Merci beaucoup d'avoir pris du temps pour m'aider !
Je vais essayer de regarder tout cela.
Cordialement.


