Inscription / Connexion Nouveau Sujet
DM programmation linéaire.
Bonjour. J'ai un petit (non, énorme soucis). J'ai pas mal de difficulté en mathématiques et ça fait plus d'une semaine que je dois faire un DM. Mon prof nous a laissé 1 mois (autrement dit je dois le rendre pour la rentrée). Le problème c'est que je patoge totalement dans la semoule. La programmation linéaire et les systèmes d'inéquations, ce n'est pas vraiment mon truc. Alors si quelqu'un peut m'aider. Sachant que le sujet est :
Le gérant d'un hotel souhaite renouveler le linge de toilette de son établissement. Il a besoin de 90 draps de bain, 240 serviettes et de 240 gants de toilettes.
Une première entreprise de vente lui propose un lot A comprenant 2 draps de bains, 4 servviettes et 8 gants de toilette pour 30€.
Une deuxième entreprise de vente lui propose un lot B comprenant 3 draps de bain, 12 serviettes et 6 gants de toilette pour 60€.
On me demande ensuite de traduire par un système d'inéquations les contraintes auxquelles satisfont x et y pour que le gérant ait suffisament de drap bain, de serviettes et de gants de toilettes. Ensuite de prouver que le système précédent est équivalent à :
x ≥ 0
y ≥ 0
2x + 3 ≥ 90
x + 3y ≥ 60
4x + 3y ≥ 120
Après, on me demande toute une série de question sur le polygone des contraites.
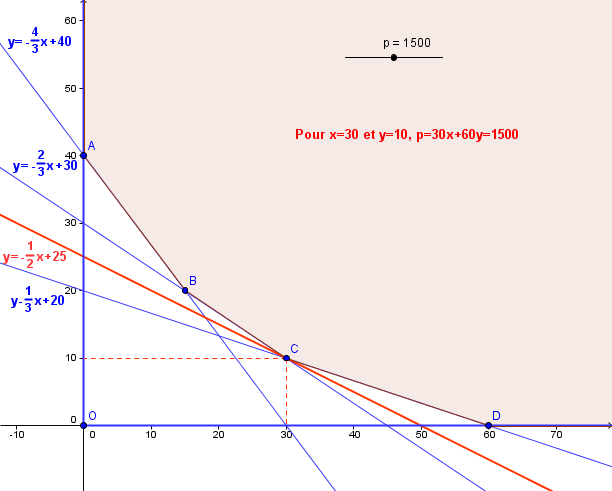
( graphique )
Et enfin, d'optimiser la dépense..
Merci de m'aider.
Bonsoir , Make-noise !... Est-ce que tu as -vu le rapport , je veux dire est-ce que tu as fait la comparaison , entre l'énoncé et le système donné des inéquations ?...
Mis à part le fait que tu aies " pas mal de difficultés " en maths, as-tu déjà lu et RELU cet énoncé ?... parce que je peux t'aider à condition que tu participes sérieusement ...
Qu'en penses-tu ?
Bonjour,
On appelle le nombre de lots
et
le nombre de lots
Avec les contraintes de l' énoncé et
doivent vérifier le système suivant:
Ou encore:
A traduire sur un graphique...

Je ne demande qu'à comprendre. Seulement avec 5 de moyenne, c'est parfois difficile de s'en sortir toute seule. (même en pensant 3h avant chaque DS est avoir des mauvaises çadémotive, mais je suis motivé là! Sachant que je révise jamais la veille bien sûr).
C'est avec un bon état d'esprit que l'on peut se mettre à travailler ...Remarque bien qu'il ne suffit pas d'être motivée, il faut participer, comme je te le disais plus haut . C'est peut-être pour cela que tu ne réussis pas bien à ton goût .
Comme te l'a expliqué le correcteur ci-dessus, on appelle x le nombre de lots A que l'on va acheter , et y le nombre de lots B achetés en même temps . On envisage donc d'acheter ces lots en une certaine quantité , qui sera forcément supérieure à 0 .
C'est pourquoi les 2 premières inéquations seront :
x > ou = 0
y > ou = 0 . Est-ce que ça va jusque là ?...
Oui, j'ai compris jusque là.
Je comprend le 90 mais pas pour le 2x + 3
Pareil pour le 60 mais pas pour le x + 3y
Egalement pour 120 mais pas pour 4x + 3y
Ne va pas trop vite .
Si on considère les besoins de l'hôtel, il lui faut 90 draps : or le lot A en apportera 2 , le lot B en apporterait 3 , donc il lui faut en acheter :
2 * x + 3 * y au minimum pour avoir les 90 nécessaires ,
donc il nous faudra : 2 * x + 3 * y supérieur ou égal à 90
C'est bien la 1ère inéquation .
Peux-tu vérifier les suivantes , sur le même modèle ?
Le besoin de l'hotel est de : 240 serviettes.
Le lot A en apporte : 4 serviettes
Le lot B en apporte : 12 serviettes.
Donc : 4x + 12y au minimum pour avoir les 240.
Soit : 4x + 12 y supérieur ou égale à 240
Es-ce ça ?
La troisième :
Le besoin de l'hotel est de : 240 gants
Le lot A en apporte : 8 gants
Le lot B en apporte : 6 gants
Donc : 8x + 6y au minimum pour avoir les 240.
Soit : 8x + 6y supérieur ou égale à 240
J'èspére que c'est ça..
Tes espérances sont réalisées ... Tu peux également simplifier...
Tu vas maintenant attaquer le graphique, pour tracer une représentation de ces inéquations .
Pour plus de facilité (pour toi) , transforme ces 3 dernières inéquations (simplifiées) sous la forme que tu connais bien : y > = a*x + b
Je t'ai dit : représentation graphique de ces inéquations , après les avoir écrites sous la forme : y > = .....
Montre moi déjà les équations : on en parlera après !
Je t'avais demandé :
écrites sous la forme : y > = .....
et aussi :
3 dernières inéquations (simplifiées)
"Vox clamans in deserto ..."
Tu as :
2x + 3y ≥ 90 On garde : 2x + 3y >= 90
4x + 12y ≥ 240 On simplifie : x + 3y >= 60
8x + 8y ≥ 240 "" 4x + 3y >= 120
et maintenant on écrit y = 30 - 2x/3
y = 20 - x/3
y = 40 - 4x/3
Ces 3 équations (affines) sont à tracer dans un repère orthonormé .
Bonjour. Voilà déjà 30 min que j'essaye de comprendre la deuxième partie de l'exercice.
On a fini hier, en disant que les équations affines étaient : y=30-2x/3
y=20-x/3
y=40-4x/3
Le prof me demande ensuite de prouver par un bref calcul que D1 (2x+3y=90) et D2 (x+3y=60) sont sécantes, D2 et D3 (4x+3y=120) sont sécantes, D3 et D1 sont sécantes.
Il faut que j'utilise a'b-ab' ?
Et que faut-on des équations affines d'hier, trouver à la fin (mise au dessus) ?
Bonjour . Voilà, c'est bien, ...tu es revenue, et ça repart !...
Avec ces équations , on va chercher imédiatement , les points d'intersection demandés ...
Pour obtenir les abscisses (puis ensuite les ordonnées) des points d'intersection, tu écris simplement : y1 = y2 , soit
30 - 2x/3 = 20 - x/3 ---> x = 30 ---> y = 10
Tu peux continuer pour les autres points ?...
Mais as-tu construit (plus simplement tracé) ces droites, et les 2 autres, sur ton graphique, pour te permettre de comprendre ce que tu fais, et ce qu'on te demande ?...
Comment puis-je tracé des droites simplement avec des équations, il me faut bien des points de coordonnées ?
Et je ne comprend pas y1=y2 .. Je n'ai jamais vu cette méthode :s
Honte à moi
Si deux droites ( D1 et D2) d'équation y1 et y2 sont sécantes, elles se croisent, (!), et elles ont en commun un point .
Donc les coordonnées de ce point seront vérifiées A LA FOIS par les 2 équations . On pourra donc écrire pour trouver ces coordonnées :
y1 = 30 - 2*x/3 = y2 = 20 - x/3 , et on déterminera x ...
comme je t'ai indiqué ci-dessus.
Pour tracer une droite, il suffit de 2 points . Avec les équations que tu as , pour D1 , d'équation y1 , tu prends une valeur quelconque x=0 par exemple, tu remplaces dans l'équation et tu obtiens : y = 0 . Cela te donne un point ( 0; 30 ). Et tu en cherches un second , avec x = 45 par exemple , et cela te donne y = 0 ... 2ème point .
Tu peux donc tracer la droite (D1) .
Achtung . Les points que nous avons pour D1 sont : ( 0; 30 )et ( 45; 0 )
Tu peux déja les placer sur ton graphique, et tirer une droite entre ces 2 points . C'est D1 ...
Tu peux continuer avec (D2) , pour la tracer ensuite ... Puis ( D3) ...
La droite (D1) passe par les 2 points :
A: xA = 0 et yA = 30 (point de l'axe des y)
B: xB = 45 et yB = 0 (point de l'axe des x)
Plutôt que tes lamentations intempestives, ce qui m'intéresserait de savoir, c'est si tu comprends quelqe chose à ce que je raconte, si cela t'ouvre les yeux sur des choses inconnues, ou fait revenir à ta mémoire des notions oubliées , ...
...en un mot , si cela t'intéresse ?...et de donne envie de continuer ?
J'ai envie de réussir. La première partie est acquise, largement. J'ai ENFIN compris comment faire un système d'inéquations avec des contraintes. Mais là, le fait de passé à des équations à une droite, je suis largement perdue.
Une droite est un ensemble de points . Ces points sont repérés par des coordonnées, par rapport à une origine et des axes que tu a choisis, et qui te permettent de dessiner ces points à leur place .
Si une relation permet de relier ensemble un groupe de points, et de fabriquer avec ces points un dessin quelconque , on dira que le dessin peut être éxécuté grâce à la relation, en fonction de la relation . On dira donc , dans l'autre sens, que cette relation est une fonction qui permet d'obtenir le tracé du dessin .
Si par exemple, la relation dont je parle est :
"si on prend 30 unités de longueur , et que l'on en retranche les 2 tiers de la longueur choisie sur l'axe des x, on obtient la longueur correspondante sur l'axe des y ..."
ce qui s'écrit : y = 30 - (2/3)*x .
Ce qui est inscrit ci-dessus est l'équation de la droite AB tracée plus haut .
Moi j'ai trouver
a'b-ab' inégale à zéro, elles sont sécantes
Donc pour D1 et D2
a'b-ab' = 2x3-1x3=6-3
Inégale à zéro, donc elles sont sécantes  ?
?
J'ai peut-être un peu mélangé les inéquations, avec les droites ...
On ne peut pas tout écrire ...
Les inéquations sont là pour poser les problémes. Elles indiquent toutes les 5 que l'on voudrait que les réponses à choisir soient à la fois inférieures ou égales, ou bien supérieures ou égales, à certaines quantités .
Comme on ne peut pas tout faire ensemble, on considère d'abord les équations qui nous indiquent les limites à ne pas franchir , quitte à ajouer, par la suite sur le dessin, les hachures qui condamneront les zones à ne pas utiliser .
Perso, grâce a a'b-ab', j'ai trouver qu'elles étaient sont sécantes.
De plus, je dois calculer des points d'intersections, je vais surement utiliser la méthode de la combinaison
..
Oui, bien sûr, elles sont sécantes, mais on ne sait pas où avec cette méthode !... Je préfère la mienne qui me donne tout-de-suite les coordonnées, et dont il faudra bien que tu te serves ensuite ...
Tu fais comme tu veux ...
J'ai fini mon DM. Bizarrement c'est tout venu d'un coup!
En tout cas, merci de votre aide. ça m'a été précieux 
C'est parfait ... Toi qui disais avoir pas mal de difficultés en maths !...
Pourras-tu , quand tu en auras le temps, me donner l'énoncé relatif à la dépense ... Non pas ce que tu as fait, mais seulement ce qui est proposé et demandé aux élèves . Merci .
Bonsoir C... Je ne sais pas pour qui tu as envoyé ce dessin ?...
Merci, si c'était pour moi, mais ce n'est pas ce que je voulais .
En ce qui me concerne , j'avais fait complètement ce qui était demandé (dessin et calcul), et je voulais que la demanderesse (?) me donne l'énoncé concernant l'optimisation de la dépense , qu'elle avait signalé dans une " pirouette " ...