Inscription / Connexion Nouveau Sujet
DM : Suite récurrente
Bonjour à tous !
Tout d'abord, je vous remercie pour votre lecture et le temps que vous prenez pour m'aider!
Donc, voici le problème : je doit rendre un devoir maison pour la rentrée. Ce devoir ce compose de deux parties distinctes. Je vais donc aborder ici la première partie, qui est la partie que j'essaye de résoudre depuis ce matin.
L'énoncé est le suivant :
A)Expression du terme de rang n d'une suite récurrente :
On considère le suite récurrente (Un) de premier terme U0=0 et telle que pour tout entier naturel n, (Un+1)=Un+2n-11
1) A l'aide d'un tableur, calculer et représenté graphiquement les 20 premiers termes de la suite. Le nuage de point a t-il une particularité? Si oui laquelle ?
Alors, j'ai réalisé tout cela, et la courbe décroit tout d'abord jusqu'à n=5 (=-25) puis ne cesse alors de croitre. Ce qui si je ne m'abuse signifie que la suite converge vers -25 sur [0;5], puis diverge vers +infini sur [5;+infini]. Ce qui me semble très étrange !
2)n étant donné, on peut calculé la valeur de Un si on connait la valeur de Un-1, on voudrait à présent pouvoir calculer, pour n'importe qu'elle valeur de n, la valeur de Un sans pour autant connaitre celle de Un-1. Pour cela, il faut disposé d'une formule donnant Un en fonction de n.
a) A l'aide des observations faites dans la première question, conjecturer une formule donnant, pour n'importe quel valeur de n, Un en fonction de n.
C'est ici que commence mes ennuis, pourtant je trouve la question simple ! j'ai tout d'abord essayé la relation de récurrence Un+1-Un, mais le résultat trouvé est -2, et les résultats sont incorrecte par rapport au graphique. Il faut d'ailleurs utiliser les informations de ce graphique, mais je ne voit pas comment. Bien que je sente que l'on doit retomber sur une suite arithmétique, ou quelque chose qui s'y apparente.
b) Démontrer cette formule
Comme je vous l'ai dit ci-dessus, la formule trouvée Un=U0-2n, ne correspond pas du tout aux résultats du tableau.
B) Etude du comportement d'une suite de récurrence :
On considère la fonction f définie sur [-(3/2);+infini] par : f(x)=RACINE(2x+3)
On donne la suite Un définie par : U0=0 et Un+1=RACINE(2Un+3)
1) a) Construire le graphique de la fonction f ainsi que les trois premiers termes de la suite Un.
Cela a été fait, mais je trouve les résultats étranges compte tenu de la question suivante :
b) Par simple lecture graphique conjecturer pour donner un majorant, un minorant et le sens de variation de la suite Un.
D'après les trois premiers termes que j'ai trouvé, Un est croissante, n'a pas de majorant sur les 3 premiers termes, et de même si l'on continue. Et a un minorant en 0. j'aimerais vous montrer les graphiques, mais comment faire ?
Pour le reste du B), je n'ai pas encore passer assez de temps dessus, je le posterais donc plus tard dans ce post, si c'est possible (ou faut il ouvrir un autre topic ?)
Merci d'avance pour vos réponses !
PB
Bonjour,
a)Ta courbe semble être une parabole.
Donc on peut conjecturer que avec
des coefficients à déterminer.
donc
donc
donc
On en tire:
et la formule conjecturée serait
b) Reste à la démontrer par exemple par récurrence.
L' initialisation est faite.
Si , alors:
et l' hérédité est prouvée.
Salut cailloux ! Et merci de ta réponse
Ma courbe est effectivement une parabole, donc tu as raison.
Par contre, dans tes calculs tu prend U1=-11, mais la formule est Un+1=Un+2n-11 donc U1=0+2*1-11=-9 non ou alors je n'ai pas tout compris ?
Ensuite, en ce qui concerne la première question, la particularité que j'avais mise en évidence est-elle juste ? ou alors dois-je juste mettre que la particularité de la courbe est qu'elle forme une parabole ??
Voilou !
PB
donne avec
:
Avec :
Pour la particularité, il s' agit bien du fait que le nuage de points semble être sur une parabole, justement pour conjecturer que
Autant pour moi ! Je suis tomber dans le panneau ! Mais, je doit donc refaire la courbe qui est alors fausse !
Mais d'après les premiers "nouveaux" calculs, cela reste une parabole.
Encore merci !
PB
En ce qui concerne les questions 1)a) et 1)b) de la partie B), je pense que comme il est demander de seulement illustrer les 3 premiers termes de la suite (Un), on peut conjecturer qu'un maximum est atteint en U3 qui vaut 3 (en arrondissant)la minimum restant U0=0 est le sens de variation reste donc croissant. Cela permet alors de comprendre la question 2 :
2)a) Montrer que si 0<x<3 alors 0<f(x)<3 (les signes sont inférieurs ou égal).
Mais, d'après le graphique, pour f(x) j'ai utilisé les 10 premiers termes, cela est incorrecte sauf si l'on considère f(x) sur les 4 premiers termes. Or la condition est que x soit compris entre 0 et 3, l'affirmation est donc exacte, mais concrètement, comment le démontrer mathématiquement ?
b) Si Un appartient à [0;3], que peut on dire du terme suivant ? En raisonnant de proche en proche, justifier alors que : pour tout n appartient à N (entier naturel), 0<Un<3 (les signes sont inférieur ou égal)
A partir de cela considérez vous que mon hypothèse quand à la réponse du 1)b) soit juste ? Ensuite, que signifie le raisonnement de proche en proche ? Mais, sachant que pour (Un) compris dans intervalle [0;3], avec dans cet intervalle (Un) minorée par 0 et majorée par 3, faut-il autre chose pour prouver que 0<Un<3 ?
Merci d'avance pour vos réponses
PB
B)1)a) Il faut faire un dessin:
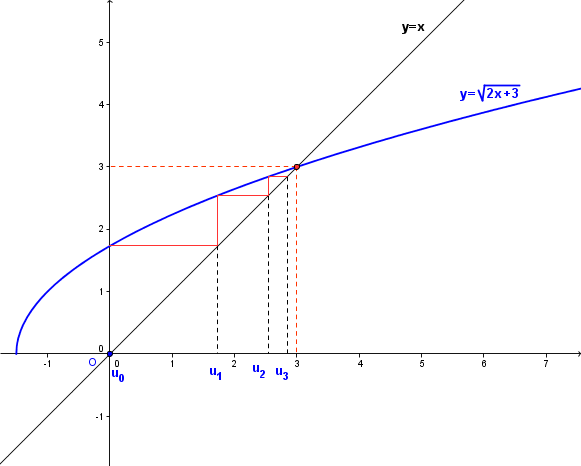
1)b) On peut conjecturer que:
est croissante.
converge vers 3.
2)a) est croissante sur
Donc si , alors
C' est à dire
Donc si , alors
2)b) Si , alors
Comme , on est donc certain que pour tout
,
C' est un raisonnement par récurrence qui ne veut pas avouer son nom ...
Hum c'est bien fourbe ^^!
Mais c'est une excellente idée que de prendre la démonstration graphique ! car après avoir réalisés quelques essaies infructueux cela m'étais impossible par le calcul du moins pour la démonstration enfin bref... merci beaucoup !
Je vais maintenant me pencher sur les dernières questions de l'exercice, histoire de voir ce que je peut en dégager, mais cela me semble un peut "tordu".
Encore merci pour ton aide
PB
Alors, en progressant plus loin dans l'exercice, il me vient une question. Je viens de regarder dans mes cours et exercices, mais je ne vois pas de configuration similaire, alors je pose la question.
Mais avant cela, énonçons les questions :
3) a) Montrer l'égalité :
Un+1-Un= ((3-Un)(Un+1))/(Racine(2Un+3)+Un
Donc, ici, aucun problèmes, c'est bien le résultat que je trouve.
b) En déduire le sens de variation de la suite (Un)
Ici, je me pose la question de la méthode : comment aborder ce calcul ? Faut-il considérer le calcul comme une fonction, mais dans ce cas que mettre à la place de Un ? La résoudre tel quel, certes mais comment, car il apparait que Un+1-Un ne donne pas de résultat exempts de Un ! Pourrait-on me donner une piste de recherche s'il vous plait ?
PB
Hum intéressant, je ne savais pas que l'on pouvait prouver de la sorte, le sens de variation d'une suite, j'ai donc grâce à toi un nouveau moyen de résoudre les problèmes sur les suites merci bien !
Entre temps, j'ai chercher la fin de l'exercice, mais là encore (décidément je me fait peur) j'ai rencontrer quelques difficultés. Mais donnons dans un premier temps le sujet :
4) a) Montrer que pour tout entier n :
Un+1-3=(2(Un-3))/(
(2Un+3)+3)
et en déduire :
[Un+1-3]
2/3[Un-3] ici les [] sont des valeurs absolues, je n'ai pas trouvé les touches correspondante, mais j'en est tout de même trouvé quelques unes !
Donc ici, pas de problème pour la première partie, mais je ne comprend pas trop ce qu'il faut faire avec les valeurs absolue, et je ne vois pas comment prouver l'inégalité.
b) Justifier alors que : (toutes les [] sont ici des valeurs absolues)
[U0-3]3 ; [U1-3]2 ; [U2-3]4/3 ; ..... ; [Un-3] 2
(2/3)^n-1
Cela s'apparente à une somme de suite, mais cela me perturbe, on doit à mon avis ré-exploité les résultats de la questions 3), ainsi que ceux de la réponse 4)a), mais je ne vois pas comment (je dois bien avoué que les valeurs absolues me gênent).
c) Déduire que la suite (Un) est convergente et donné sa limite.
Alors ici, je pense que grâce aux résultats obtenu dans le 4)b) la suite converge vers 3, cela doit certainement être prouvable à partir des résultats obtenus dans la 4)b), mais reste à résoudre le problème de cette question b).
Merci pour ton aide
PB
On a donc
Le dénominateur est supérieur à 3.
Donc
On sait que et
donc et
On peut donc écrire:
Pour la suite, on fait encore une récurrence sans l' avouer:
donc
donc
donc
donc
On a donc "prouvé" que:
Or
Les gendarmes permettent d' écrire que:
Autrement dit que:
Oula c'est tout de même un peut tordu tout cela !
En tout cas merci pour ton aide précieuse tout au long de cet exercice, c'est vraiment très aimable de ta part, ça fait toujours plaisir de pouvoir comprendre ce que l'on fait et comment faire !
Bonne continuation
PB
Bonjour, je sais que sa date un peu mais bon j'ai le même sujet donc autant en profiter. J'aimerais savoir comment mettre la suite dans le tableur svp je suis vraiment perdu ! Merci.
Bonjour,
Voici ce que ça donne:
Mais pour réaliser ce tableau, tout dépend du tableur dont tu disposes...
Bonjour, merci j'ai enfin compris. Par contre, je n'arrive pas à renommer colonne B en u(n). Comment avez vous fait ?
Bonjour besoin d'aide ici svp 
désintégration radioactive et équations différentielles (TS)
Annuler
connectez vous