Inscription / Connexion Nouveau Sujet
(Double) dérivation
Bien le bonsoir à toute la communauté. :]
Je suis nouvelle parmi vous, et je peine à arriver au bout d'un 'sympathique' 'petit' travail de mathématiques récolté pour avoir échoué en fin d'année.
Je vous propose ici un de mes (trop) nombreux énoncés, à savoir qu'il s'agit là d'une dérivée qui sera utilisée dans une étude de fonction, et que la recherche de la ou des racine(s) éventuelles des fonctions dérivées obtenues est donc essentielle.
1) Fonction de base :
racines obtenues : f(x) = O x = +1 et -1
2) Fonction dérivée première (mes résultats) :
racines obtenues : f'(x) = O x = +1 et -1
=> Ici se situe mon problème : je cale sur le résultat de ma dérivée seconde, qui ne me semble en rien probant... Je retranscris donc mon développement ici, dans l'espoir que quelqu'un puisse m'aider à mettre le doigt sur mon erreur.
3) Fonction dérivée seconde (idem) :
Pour ce qui est des racines de cette fonction dérivée seconde (qui n'est pas forcément correcte), j'obtiens le chiffre 0. Ensuite, afin d'établir mon tableau de signes, il me faut les racines de ... Et, cela va sans doute paraître un peu ridicule aux plus matheux d'entre vous
, mais cet exposant quatre m'effraie et je ne sais qu'en faire. x] La fonction possède-t-elle les mêmes racines que la fonction usuelle
?
En vous remerciant d'ores et déjà pour l'attention portée à ce léger souci !
Bonjour,
Ta dérivée première ne s' annulle pas: (strictement).
Le domaine de définition de ta fonction est et
ne s' annulle jamais non plus.
! Et bonsoir cailloux Heu. XD Déjà, si j'ai bien tout suivi, je dois comprendre que ma fonction dérivée seconde n'est pas , mais bien
?
...Sinon, j'ai bien compris vos explications quant aux domaines et à la valeur interdite de 0 ici, mais je n'arrive toujours pas, dans ce cas, à trouver mes racines... :/ (Ne me lynchez pas, pitié YwY)
f''(x ) > 0 pour x <0
f''(x ) < 0 pour x >0
tu peux d aileurs , d entree prouver que f est impaire , ça te restreind le domaine d etude
Je suis désolée, je vais m'enfoncer encore un peu plus, mais soit.
Je n'arrive pas à comprendre comment vous avez obtenu ... Et je suis toujours bloquée sur la méthode pour trouver mes racines. (Oui, vous pouvez me maudire, il n'empêche que je suis complètement larguée... J'ai l'impression que je vais devoir recommencer mon étude en entier. Ô, joie.)
Merci pour ces permières pistes de réponse :]
oups et re oups
f''(x) n est pas egal a -2x/x^3 mais à
-2/ x^3 ( qui est d ailleurs egal pour x different de 0 au -2x/x^4 que tu trouvais au depart ! )
Melandine, ton calcul de la dérivée seconde est laborieux mais juste: simplifie par x numérateur et dénominateur de ta fraction et tu as bien le résultat de Spmtb.
Pour tes questions sur les racines, tu t'intéresses à ton dénominateur de f'':
On a aussi, même si cela ne sert à rien pour cette étude-ci:
Donc tu n'as pas vraiment besoin d'un tableau de signes pour déterminer le signe de f''(x) qui est l'opposé du signe de x:
tu as ainsi prouvé les résultats de Spmtb.
*tilt !*
Désolée, j'ai voulu aller trop vite. :] Un tout grand merci pour votre patience. x']
Reste ce problème de racines. :'D J'ai relu vos réponses, me suis creusé ma cervelle de moineau, et... Etant donné qu'il est donc impossible d'annuler la fonction dérivée seconde , comme vous l'avez énoncé plus haut, cela signifie donc qu'il n'y a pas de racines pour cette fonction... Tout comme pour ma fonction dérivée seconde (?)
Dans ce cas, comment faire avec mes tableaux de signes... ? Car j'ai peur que si je n'en élabore pas, ma prof de maths me le compte comme une pénalité... Chercher le domaine, sans doute... Sans racines, cela signifierait donc, dans un premier temps, qu'il n'y a pas d'exremum à ma fonction de base, et, dans un deuxième temps, qu'il n'existe pas de point d'inflexion... Et étant donné que ma fonction de base est impaire... Il ne me reste plus qu'à compter sur mes asymptotes pour pouvoir tracer mon graphe. (Une verticale en , et une oblique en
, si mes calculs sont bons.)
...Complètement à côté de la plaque ou... ? XD
Re bonsoir,
Tu peux déjà t' occuper des variations de ta fonction.
sur
donc ta fonction est strictement croissante sur
Par contre, on ne sait pas quelles sont les questions posées dans ton exercice...
S' agit-il d' une étude de fonction? auquel cas, il faut étudier les limites aux bornes de l' ensemble de définition, les asymptotes... ou autre chose?
On ne peut rien vous cacher cailloux, il s'agit bel et bien d'une étude de fonction. :'D
En tout, voici ce qu'on me demande : le domaine de ma fonction de base, la parité de cette même fonction, les limites aux bornes de l'ensemble de définition, les asymptotes éventuelles donc, le signe de ma fonction de base ainsi que ses racines éventuelles, l'ordonnée à l'origine, l'existence et la détermination de f'(x) ainsi que f''(x) (après avoir déterminé les racines éventuelles), et enfin un tableau de variation récapitulant les résultats précédents avec croissance et concavité de f(x) avant le tracé final de la courbe.
(Une véritable étude de fonction en pure et due forme, donc. :])
Je crois avoir saisi le principal. Encore un dernier merci à tous, je m'y remets dès demain.
f" est un quotient (2 expressions possibles) donc tu veux faire un tableau de signes pour étudier son signe. Tu peux évidemment mais avec
f"(x)=(-2)/x^3 par exemple, le numérateur est -2 donc strictement négatif pour tout x, et donc le signe de f"(x) est directement l'opposé du signe du dénominateur (d'après la règle des signes d'un quotient).
Or le signe du dénominateur x^3=x^2*x est le signe de x pour x
0 (car x^2>0 et règle des signes d'un produit).
Conclusion (toujours la même): le signe de f"(x) est l'opposé du signe de x.
Bon, en commençant par le commencement;
-Domaine de définition:
-Parité
Le domaine de définition est symétrique par rapport à la valeur 0.
et
La fonction est donc impaire et la courbe
admet l' origine comme centre de symétrie. On pourrait se limiter à une étude sur
-Limites aux bornes de l' ensemble de définition:
* car
et
* car
Par symétrie:
*
*
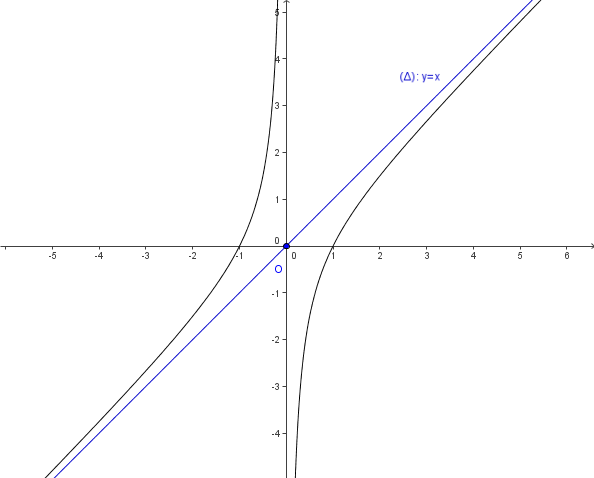
-Asymptotes:
*Des limites en 0, on déduit que la droite verticale d' équation est asymptote à
*
La droite d' équation
est donc asymptote oblique à
en
et en
-Position de la courbe par rapport à son asymptote
Si ,
et
est au dessus de
Si ,
et
est au dessous de
-Variations
est dérivable sur
:
sur
et
est croissante sur
-Dérivée seconde
est dérivable sur
et
Si ,
et la courbe tourne sa concavité vers les y positifs.
Si ,
et la courbe tourne sa concavité vers les y négatifs.
Manque le graphe...
bonsoir à tous,
cailloux >> Joli LaTeX !
Comme tu l'as dit au début, l'interêt de la parité est de ne travailler que sur la moitié de l'ensemble de définition. Pourquoi ne pas s'en servir ?
Bonsoir Sarriette,
Comme tu l' as vu j' ai utilisé le conditionnel: on pourrait se limiter...
J' ai souvent remarqué des énoncés où l' on demande d' étudier la parité et où la fonction est effectivement paire ou impaire.
Les questions suivantes sont du genre:
-Etudier les limites aux bornes de l' ensemble de définition
-Etudier les variations sur le domaine de définition
-Etc...
On peut utiliser la symétrie, mais on ne gagne rien en temps ni en simplicité.
L' idéal serait d' étudier la fonction sur une moitié du domaine et de tracer la courbe correspondante complétée par symétrie.
En pratique, je l' ai rarement vu
Oui c'est ce à quoi je pensais aussi, utiliser la symétrie tout à la fin lors du tracé.
En fait lors des questions suivantes on pourrait se limiter au domaine d'étude et non au domaine de définition.
Le pire, c' est de trainer la symétrie tout au long de l' étude:
Par exemple ici, je crois que doit chercher points d' intersection de la courbe avec l' axe des abscisses:
Soit à résoudre qui donnerait
sur
complété par symétrie avec
. Tordu non ?
Je ne parle pas des variations: suivant que la fonction est paire ou impaire, on a vite fait de se planter
Parfait ! Je viens de refaire mon étude en entier en suivant vos pistes, et vos lumières Un énooorme merci à cailloux pour son Latex très clair et complet ! :] Et évidemment un tout grand merci de même à ceux qui se sont penchés sur mon problème, toutes vos réponses m'ont été fort utiles... Je m'étais engagée sur une mauvaise voie, mais à présent tout est réglé. :]
Bonne journée à tous !
Annuler
connectez vous