Inscription / Connexion Nouveau Sujet
dur dur les DM de 1°7 ( fonctions dérivées)
salut tous le monde g un dm et g du mal a le faire alors un peu d'aide, ce serai pas de refu !
On considère la fonction f définie sur R par :
f(x) = (x-0,05)(x²-0,3x+0,02)
On désingne par Cf sa courbe représentative dans un repère orthogonal.
1°) Combien Cf a-t-elle de tangentes parallèes a l'axe des abscisses comprises entre 0,05 et 0,25 .
Bonjour,
en appliquant la formule de la dérivée de uv qui est :
(uv)=u'v-uv'
je trouve f'(x)=-x²-0.17x+0.005
Les tgtes à Cf sont // à l'axe des x pour les valeurs de x qui annulent la dérivée.
Or cette dérivée s'annule pour 2 valeurs qui ne sont pas comprises entre 0.05 et 0.25.
...sauf erreurs possibles de ma part.
Mais qq. corrigera ds ce cas.
Salut.
si x tend vers - , f(x) tend vers -
, f(x) tend vers -
si x tend vers + , f(x) tend vers +
, f(x) tend vers + .
.
On calcule, en factorisant, que f(x) s'annule pour x=0,05, x= 0,1 et x=0,2.
Donc 1 maximum local sur [0,05; 0,1]
et 1 minimum local sur [0,1; 0,2]
Donc 2 tg parallèmes à x'Ox
Je vien de me rendre compte ke je m'était tromper , g mélanger les 2 questions!
1°) Combien Cf a-t-elle de tangentes parallèles à l'axe des abscisses?
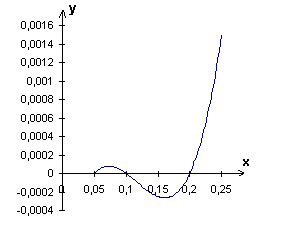
2°) Tracer la portion de Cf correspondant aus abscisses comprises entre 0,05 et 0,25 .
DESOLE !
1)
f '(x) = x² - 0,3x + 0,02 + (x - 0,05).(2x - 0,3)
f '(x) = x² - 0,3x + 0,02 + 2x² - 0,3x - 0,1x + 0,015
f '(x) = 3x² - 0,7x + 0,035
Les tangentes à Cf // à l'axe des abscisses le sont aux abscisses telles que f'(x) = 0.
f '(x) = 0
3x² - 0,7x + 0,035 = 0
x = (0,7 +/- V(0,49 - 0,42)]/6 V pour racine carrée.
x = [0,7 +/- V(0,07)]/6
Il y a donc 2 tangentes à Cf // à l'axe des abscisses.
Elles sont tangentes à Cf aux points d'abscisse:
[0,7 - V(0,07)]/6 = 0,07257...
et
[0,7 + V(0,07)]/6 = 0,16076...
-----
2)
Voir dessin.
-----
Sauf distraction.