Inscription / Connexion Nouveau Sujet
Enigmo 40 : A table ! 


Bonjour,
pour fêter la Saint-Jamo, j'ai décidé d'inviter quatre amis pour diner un soir. Nous allons donc nous retrouver cinq à table.
Mais chez Jamo, on sait recevoir ! 
Je dispose d'une table ronde de 2 mètres de diamètre, sur laquelle je place une magnifique nappe jaune pâle.
Pour chaque convive, un set de table rouge.
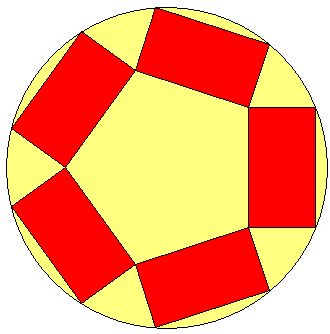
Les sets de table, tous identiques, sont rectangulaires et disposés comme le montre la figure : 2 coins sur le bord de la table, et les 2 autres coins en contact avec les coins des sets de table voisins.
Les dimensions des sets de table sont tels que l'aire occupée par les sets de table sur la table soit maximale.
Question : donner la longueur et la largeur d'un set de table pour que ce maximum soit atteint. Je veux les valeurs en millimètre arrondies à l'entier.
Remarque importante : toutes valeurs qui seront données dans la mauvaise unité ou avec la mauvaise précision ne seront pas acceptées, même si la réponse est accompagnée d'une démonstration exacte. Cette consigne est donnée dans un souci d'équité, et j'estime qu'il faut savoir aller au bout d'un tel calcul avec une précision donnée.
Bon appétit !

 Bonjour,
Bonjour,
une petite énigme de géométrie matinale... miam !
En considérant le pentagone central avec de la trigonométrie et Pythagore on arrive à l'étude d'un maximum d'une fonction brute assez moche : où x est le rayon du pentagone. (pas envie de simplifier!)
Le maximum est alors réalisé si x coïncide avec la largeur du rectangle (et non pour un set carré).
Une valeur (approchée) r de ce maximum nous fournit les dimensions du set, L= et l=
ce qui donne à la précision exigée L618 mm et l
526 mm (pour une aire approchée 3249 mm²).
Merci pour l'enigmo et bon appétit aussi !
 Bonjour,
Bonjour,
A priori, on ne sait pas quel côté est la longueur et quel côté est la largeur d'un set.
Je parlerai plutôt de largeur et de profondeur: largeur de gauche à droite devant chaque convive, et profondeur dans le sens du rayon de la table.
Pour une surface de set maximale:
largeur  618 mm
618 mm
profondeur  526 mm
526 mm
Merci pour l'énigme,
gloubi 
 Après de savoureux calculs je trouve :
Après de savoureux calculs je trouve :
L= 618 mm
l= 526 mm
(arrondis au nombre entier de mm le plus proche)
 Soit D le diametre du cercle circonstrit (en mm) aux coins des sets de table (les plus proche du milieu)
Soit D le diametre du cercle circonstrit (en mm) aux coins des sets de table (les plus proche du milieu)
Dans ce cas, on, peut calculer la longueur des sets avec pythagore: D*sin(36°)
La largeur vient aussi rapidement avec le même théorème: (1/2)(2000-D)cos(36°)
d'où l'aire:
(1000-D/2)cos36*Dsin36
On dérive pour avoir le max:
A'=-D+1000cos36sin36
elle s'annulle en D=1000, donc à la moitié
Dans ce cas, la longueur est égale environ à: 588 mm
Et la largeur environ: 405 mm
 bonjour
bonjour
la longueur de chaque set (le côté qui est une corde du cercle) est 908 mm
la largeur de chaque set est 561 mm
conjecture : la largeur est égale à la distance qui sépare le centre des coins qui en sont le plus proches
construction : d'un point du cercle, tracer le diamètre et la corde qui fait 9 degrés avec ce diamètre; l'intersection de la corde et de la médiatrice du rayon partant du point est un coin du set; la longueur du set est le côté du pentagone dont le rayon est la distance entre le centre et le coin du set
 Soit R=1m le rayon de la table, r le rayon du cercle intérieur circonscrit au pentagone formé par les cotés intérieurs des rectangles, L la longueur et l la largeur de ces rectangles. On a alors L=2r*sin(pi/5), donc Ll=2rl*sin(pi/5) et si l'on écrit que les coins extérieurs des rectangles sont sur le grand cercle, (r+l*cos(pi/5))^2+(lsin(pi/5))^2=R^2 que l'on peut encore écrire: 2rl(1+cos(pi/5))=R^2-(r-l)^2.
Soit R=1m le rayon de la table, r le rayon du cercle intérieur circonscrit au pentagone formé par les cotés intérieurs des rectangles, L la longueur et l la largeur de ces rectangles. On a alors L=2r*sin(pi/5), donc Ll=2rl*sin(pi/5) et si l'on écrit que les coins extérieurs des rectangles sont sur le grand cercle, (r+l*cos(pi/5))^2+(lsin(pi/5))^2=R^2 que l'on peut encore écrire: 2rl(1+cos(pi/5))=R^2-(r-l)^2.
On voit sur cette forme que l'aire Ll, proportionnelle à rl sera maximum pour r=l, soit r^2=R^2/2(1+cos(pi/5) et Ll=R^2*sin(pi/5)/(1+cos(pi/5))=R^2*tan(pi/10).
Puisque tan(pi/10) est légèrement supérieur à pi/10, l'aire recouverte par les 5 rectangles sera un peu supérieure à la moitié de la surface de la table pi*R^2.
Plus précisément, Ll=0,3249 m2, soit r^2=0,2764 m2 ou r=0,5257 soit une largeur arrondie (au plus proche, ce que ne précise pas l'énoncé) à 526 mm et une longueur arrondie à 618 mm
 bonjour
bonjour
Sauf erreur, jamo, tu aurais du demander les valeurs exactes, et non arrondies...
--------------------
maintenant, je peux me tromper mais je trouve :
¤ une longueur de
¤ une largeur de
¤ pour une surface de
---------------------
soit en mm arrondis :
¤ une longueur de
¤ une largeur de
¤ pour une surface de
A vérifier
Bon a 

 Il peut être intéressant, d'ailleurs, de chercher à généraliser le résultat en prenant, non plus 5 sets de table, mais N sets de table
Il peut être intéressant, d'ailleurs, de chercher à généraliser le résultat en prenant, non plus 5 sets de table, mais N sets de table
Je dispose d'une table ronde de 2 mètres de diamètre, sur laquelle je place une magnifique nappe jaune pâle et, pour chacun des N convives, un set de table rouge.
Les sets de table, tous identiques, sont rectangulaires et disposés de telle sorte qu'ils ont 2 coins sur le bord de la table, et les 2 autres coins en contact avec les coins des sets de table voisins.
Les dimensions des sets de table sont tels que l'aire occupée par ceux-ci sur la table soit maximale.
Question : donner la longueur et la largeur d'un set de table pour que ce maximum soit atteint.
Une fois l'énigme de jamo corrigée, ceux qui désirent creuser cette question pourront s'y atteler...
y'a rien à gagner, sinon ma considération

-----------------------
ah si, la subsidiaire culturelle
 :
:

Pourquoi cette image ?

 je suppose que tout le monde l'a déjà trouvé, mais l'angle entre 2 rectangles est de 360/5 = 72°...je ne sais pas si ça va m'aider hihi po facile
je suppose que tout le monde l'a déjà trouvé, mais l'angle entre 2 rectangles est de 360/5 = 72°...je ne sais pas si ça va m'aider hihi po facile
 Re
Re
Ayant un peu de temps pendant le séchage de deux couches de vernis à bois  , je vais détailler mes réponses :
, je vais détailler mes réponses :
Pour des raisons de symétrie, les deux coins intérieurs du set sont sur les rayons des secteurs angulaires d'angle 2pi/5
Ainsi, on peut simplifier le problème en le ramenant dans un secteur de pi/5 et en cherchant à maximiser le rectangle ABCD où OA=x
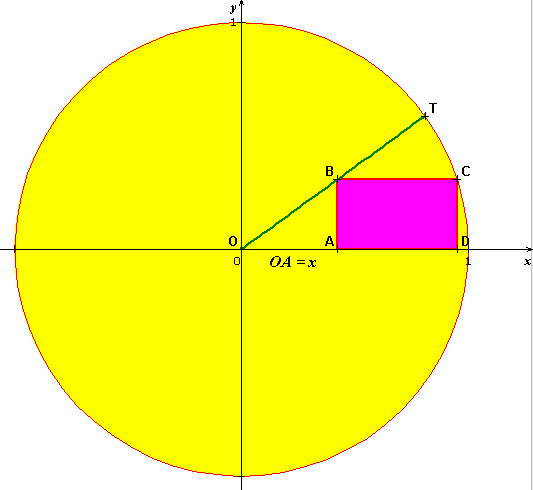
et, puisque tan(pi/5) va être utilisé fréquemment, je pose t = tan(pi/5)
---------
OT est tel que y = tx et B est sur OT => B ( x ; xt ) => AB = tx
C est sur le cercle x²+y²=1 et d'ordonnée yB => C ( racine(1-t²x²) : tx ) => AD = BC = racine(1-t²x²) - x
la surface cherchée vaut donc S(x) = 2.AB.AD
S(x) = 2tx( racine(1-t²x²) - x )
S'(x) = 2t( 1-2t²x²-2xraxine(1-t²x²)-x)/racine(1-t²x²)-x) qui s'annule pour :
1-2t²x²-2xracine(1-t²x²)-x) = 0
2xracine(1-t²x²)-x) = 1-2t²x² où je pose X = x²t² et élève au carré
4(X/t²)(1-X) = 1-4X+4X²
X² - X + t²/4(1+t²) = 0 et, puisque t est une tangente, t²/(1+t²) = sin²
X² - X + sin²/4 = 0, de delta = 1-sin² = cos²
dont la seule solution acceptable ici est X = (1-cos)/2 = sin²(pi/10) qui fournit x = racine(X)/t
x = sin(pi/10)/tan(pi/5) et on déduit AB = sin(pi/10)
Le plus dur est fait : y'a plus qu'à reporter dans AD et S pour trouver les valeurs simplifiées que j'ai postées ( et dont je n'ai plus le brouillon  )
)
--------------
Je suis persuadé qu'un "vrai" matheux va nous résoudre ça élégamment rien qu'avec de la géométrie ( je pense à piepalm, par exemple,  )
)
--------------
La complémentaire, celle à N sets de table, postée au-dessus, devrait être sympa aussi...

 Bonjour Jamo, et bon appétit.
Bonjour Jamo, et bon appétit.
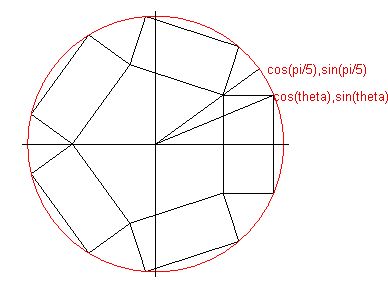
Le coin nord-est du set a pour coordonnées cos(theta) et sin(theta) (voir dessin).
(L'unité est provisoirement le mètre, theta est entre 0 et Pi/5).
Après simplifications, je trouve:
La largeur du set est sin(Pi/5-theta)/sin(Pi/5).
La longueur: 2sin(theta)
L'aire: (cos(2theta-Pi/5)-cos(Pi/5))/sin(Pi/5).
Cette aire est donc maximale pour cos(2theta-Pi/5)=1, donc pour theta=Pi/10.
En reportant dans les expressions de la longueur et la largeur, je trouve:
longueur: 618 mm
largeur: 526 mm
 bonjour,
bonjour,
soit l la largeur de chaque set, et L sa longueur
l'aire du cercle est de 
coupons le cercle en 5 parts égales d'aire  /5
/5
pour que l'aire occupée par les sets soit maximale, la somme des aires du pentagone, des 5 quarts de cercle entre chaque rectangle, et des 5 arcs de cercle doit être minimale.
aire des 5 quarts de cercle entre chaque rectangle:  xl[/sub]2
xl[/sub]2
le pentagone est partagé en 5 triangles isocèles de base L, de cotés (1-l)et de hauteur h. d'aprés pytagore, (1-l)[sub]2= h[/sub]2+ (L/2)[sub]2. d'où, l'aire d'un triangle est de (L  (L/2)[/sub]2-(1-l)[sub]2)
(L/2)[/sub]2-(1-l)[sub]2)
l'aire du pentagone est donc de: 5x aire d'un triangle.
ensuite je suis bloquée sur l'aire des arcs de cercle de rayon 1 et de longueyr de corde L
je continue + tard, j'espère ne pas nuire à la résolution de l'enigme, bonne chance à tous!
 Bonjour
Bonjour
Réponses :
largeur :
longueur :
Donc en millimètres arrondis au millimètre le plus proche
largeur : 526 mm
longueur : 618 mm
Éléments de la démonstration:
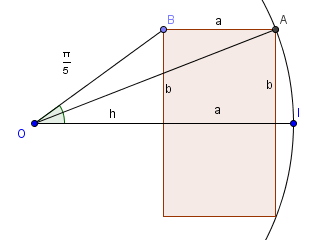
Les 10 sommets intérieurs des cinq sets sont sur un pentagone régulier, donc l'angle a pour mesure
en choisissant les notations ci-dessous
Les deux relations suivantes nous permettent de calculer le maxima souhaité
Domaine de définition :
On exprime b en fonction de a :
On résout cette équation polynômiale du second degré en b en conservant la seule racine positive :
Étudions alors la fonction , dont le maximum donnera la valeur de a pour laquelle la surface des sets sera maximale.
Fonction définie, dérivable sur [0,1], de dérivée
Dérivée continue, de valeurs de signes opposés, donc s'annule et change de signe pour au moins une valeur de a qui vérifie :
Pour résoudre cette équation, nous l'élevons au carré, mais imposons, de manière à conserver l'équivalence :
Equation bicarrée, donnant deux solutions en , dont l'une est éliminée du fait de la contrainte citée ci-dessus
La solution est rejetée, car elle mène à
en contradiction avec la contrainte.
Et donc, on conserve pour a la valeur positive :
Nous calculons alors et nous obtenons
Et la surface d'un set de table
En conclusion, les dimensions optimales du set de table sont
Passons à l'application numérique, avec et
Nous obtenons
Jamo, la prochaine fois, invite 16 convives. A 17, les calculs numériques seront un peu plus sportifs. 
 bonjour Jamo,
bonjour Jamo,
Question : donner la longueur et la largeur d'un set de table pour que ce maximum soit atteint. Je veux les valeurs en millimètre arrondies à l'entier.
longueur 1236 millimètres
largeur 1051 millimètres
 Bonjour,
Bonjour,
Voici les dimensions d'un set de table (longueur par largeur) pour que l'aire occupée par les sets de table sur la table soit maximale :
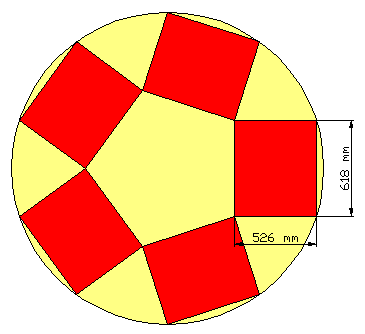
Les valeurs en millimètre sont arrondies à l'entier le plus proche : C'est le principe de l'arrondi...
Rq : J'ai longtemps hésité, car avec ces valeurs, il y a un chevauchement des sets de table de 0,24 mm. Si on ne souhaite pas avoir de chevauchement (là, c'est le technicien qui parle...), c'est à l'entier inférieur qu'il aurait fallu arrondir soit 525 mm au lieu de 526 pour la largeur.
Merci et à plus, KiKo21.
 Ma réponse: longueur:618 mm largeur: 526 mm
Ma réponse: longueur:618 mm largeur: 526 mm
pour y parvenir j'ai exprimé la largeur l en fonction de la longueur L :
Avec D le diamètre de la table.
et ensuite en exprimant l'aire d'un set de table : A=l*L
Je cherche le maximum de cette fonction :
L'aire maximale d'un set est donc : A=0.325m²
 Bonjour jamo,
Bonjour jamo,
La description de la disposition des sets de table donne comme système d'équations (l'unité de mesure étant le mètre):
On en déduit la surface d'un set de table:
Cette surface est maximale pour
Les dimensions d'un set de table sont donc:
Les dimensions d'un set de table (valeurs en millimètre arrondies à l'entier le plus proche) sont:
Longueur : 618 mm.
Largeur : 526 mm.
 Je dirais que les sets de table ont les dimensions suivantes:
Je dirais que les sets de table ont les dimensions suivantes:
Largeur: 0,525764324...m soit 526 milimètres en arrondissant à l'entier supérieur.
Longueur: 0,6179949456... m , soit 618 milimètres en arrondissant à l'entier supérieur.
L'aire occupée par les 5 sets serait 1,62534 m² sur la table en utilisant les arrondis.
J'espère que c'est juste et merci pour l'énigme !
 Bonjour,
Bonjour,
Je dirais que chaque set mesure 618mm sur 526mm.
Les valeurs exactes, si la table est de rayon R, sont respectivement et
.
Pour les trouver j'ai utilisé les valeurs exactes des cosinus et sinus de pi/5.
Ma démarche a consisté à se ramener à trouver le rectangle d'aire maximale inscrit dans un secteur circulaire d'angle 2pi/5, dont deux sommets sont sur l'arc de cercle, et tel qu'il soit symétrique par rapport à l'axe de symétrie du secteur circulaire (j'espère que c'est clair... je n'ai pas d'outil de dessin sous la main).
BA.
 re bonjour Jamo
re bonjour Jamo
je vais essayer de faire encore un énigmo avant de partir en vacances
chaque set de table est inscrit dans un secteur circulaire d'angle au centre 2 /5
/5
____________O______________________
.
.
.
.
.
A___________H___________B
. .
. .
. .
C___________K___________D
ABCD est un set les sommets C et D sont sur la circonférence de rayon 1
A et B sont les sommets communs avec les sets voisins
OK est la médiatrice de DC donc de AB et c'est la bissectrice de l'angle AOB donc l'angle AOH vaut  /5
/5
je note  l'angle COK 0<
l'angle COK 0< <
< /5
/5
CK=COsin =Rsin
=Rsin =sin
=sin donc AH=sin
donc AH=sin et AB=2sin
et AB=2sin
OK=OCcos =cos
=cos
HK=OK-OH
mais OH/AH=cotan /5=>OH=sin
/5=>OH=sin cotan
cotan /5
/5
d'où
HK=cos -sin
-sin .cotan
.cotan /5
/5
la surface d'un set est donc S( )=2sin
)=2sin [cos
[cos -sin
-sin cotan
cotan /5]
/5]
S( )=sin2
)=sin2 -2sin²
-2sin² cotan
cotan /5
/5
S' )=2cos2
)=2cos2 -2sin2
-2sin2 cotan
cotan /5
/5
S'( =0<=>tan2
=0<=>tan2 =tan
=tan /5
/5
dans l'intervalle considéré la solution est  =
= /10
/10
S passe par un maximun pour cette valeur de  et l'aire occupée par les sets est alors maximale
et l'aire occupée par les sets est alors maximale
on en déduit les dimensions demandées
L=2sin /10 m soit 618mm. par défaut
/10 m soit 618mm. par défaut
l=1/(2cos /5) soit 525mm. par défaut
/5) soit 525mm. par défaut
je me demande si je ne me suis pas trompée car cela me parait bien grand pour un set de table il est
vrai que la table est de belle taille et sans doute que Jamo tient à protéger sa belle nappe
merci Jamo pour cet énigmo
 IÔN = a avec a Î [0 ; pi/5 ]
IÔN = a avec a Î [0 ; pi/5 ]
IÔA1 = pi/5
L = 2NH = 2sin a
l = MN = OH - OK = cos a - MK.cot = cos a - sin a.cot pi/5
Donc l = sin(pi/5 - a) / sin(pi/5)
Donc l'aire des 5 sets est A = 5Ml = 10sin a * sin(pi/5 - a) / sin(pi/5)
Or sin a . sin b = 1/2 * (cos(a - b) - cos(a + b))
Alors A = 5Ll = 5cot pi/5 - 5 cos(2a - pi/5) / sin(pi/5)
Donc A' = 10 sin(2a - pi/5) / sin(pi/5)
A' = 0 ssi sin(2a - pi/5 ) = 0 ssi a = pi/10 (pi/2)
Or seul pi/10 appartient à [0 ; pi/5]
Donc L = 2sin pi/10 = environ 0,61803398875 m
De plus, l = environ 0,525731112119 m
Donc l'aire des 5 sets est : A = 5Ll = environ 1,62459848116 m²
Or l'aire de la nappe est pi x R² = pi x 1² = pi = environ 3,14159265359 m²
Donc les 5 sets représentent environ 51,72% de la nappe
La réponse à l'énigme est : Longueur d'un set : L = environ 618 mm
Largeur d'un set : l = environ 526 mm
 ma réponse est: 618 mm sur 526 mm
ma réponse est: 618 mm sur 526 mm
explication:
un set de table est compris dans un secteur de 360/5 = 72 degrés
je fais varier x de 0 à R (donc de 0 à 1 mètre) et je calcule la largeur et la Longueur en fonction de x:
Longueur = 2.x.sin(36)
largeur = - x.sin(54)
et ensuite je calcule la surface d'un set en fonction de x
à noter que les 5 sets de table ont chacun la même surface, il suffit donc de calculer le maximum de l'un.
pour avoir ce maxi, l'informatique est venue à mon secours
x=0,52573m L=0,6180326681275103m l=0,525732224217869m S=0,324919696166093m2
je m'attendais à trouver un carré.
 Bonjour,
Bonjour,
une petite maximisation numérique de la fonction
f:=r->(2*r*sin(Pi/5))*(cos(arcsin(r*sin(Pi/5)))-r*cos(Pi/5));
par Maple me donne les résultats suivant (arrondis au plus proche) :
Longueur du set : 618 mm
Largeur du set : 526 mm
Etrangement, ce maximum est atteint lorsque la largeur du set est égale au rayon du cercle passant par les points intérieurs des sets. Bizarre...
En espérant un smiley 
Merci pour l'énigme,
1emeu
 Bonsoir,
Bonsoir,
Les dimensions des set de table sont : avec L et l respectivement la Longueur et la largeur d'un set. (n'oublions pas qu'un carré est un rectangle particulier, et que de toute façon avec les arrondis on ne peut différencier le carré du rectangle
 )
)
Sans aucune conviction 
Merci pour cette énigme à laquelle je suis incapable de répondre sans informatique 
 Salut,
Salut,
Après un calcul bourrin  je trouve :
je trouve :
largeur = 618 mm
profondeur = 526 mm approximativement (En fait, comment écrire presque égal avec latex ?)

 On considère seulement un set de table qui est inscrit dans un triangle isocèle de sommet principal le centre de la table et dont les deux autres sommets sont des points du bord de la table.
On considère seulement un set de table qui est inscrit dans un triangle isocèle de sommet principal le centre de la table et dont les deux autres sommets sont des points du bord de la table.
Les deux côtés de même longueur mesurent 1 mètre (soit 1000 mm) et le dernier côté environ 1176 mm (en effet, les angles égaux mesurent 54° et l'angle du sommet principal 72°).
On construit des rectangles inscrits dans ce triangle tels que le milieu de leur largeur (ou longueur) soit le milieu de la base du triangle.
L'aire de ces rectangles est maximale si le rectangle est un carré.
En posant une inconnue, on trouve un set de table carré de côté égal à environ 296 mm.
Clôture de l'énigme
L'idée de cette énigme m'est venue suite à la lecture d'un article dont voici la fiche de présentation : ![]() .
.
Dans cet article, on étudie le problème général avec n sets de table. L'image suivante représente un demi-set de table, donc inscrit dans un secteur angulaire d'angle PI/n.
On démontre alors qu'il faut placer le point B sur la bissectrice de cet angle pour atteindre l'extremum. Je donne les formules pour AB et BC sur la figure.
Dans cet article, on démontre ce résultat à la fois avec des méthodes de lycée, mais aussi de collège !
Bravo à manpower qui remporte le mois de juin ! 
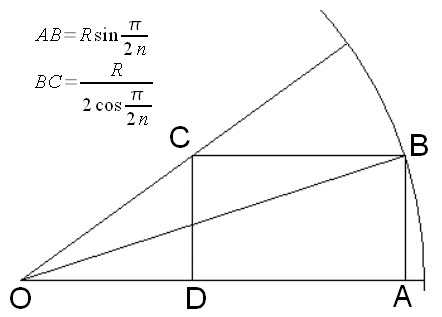
 Ach, Schade, l'énigme complémentaire est répondue... reste que la subsidiaire
Ach, Schade, l'énigme complémentaire est répondue... reste que la subsidiaire ![]() Enigmo 40 : A table !
Enigmo 40 : A table !

Bonjour,
L'image de la subsidiaire proposée par Mika représente une divinité de l'Egypte ancienne nommée Seth (mais je ne sais pas si on l'invitait beaucoup à table  )
)

Question : donner la longueur et la largeur d'un set de table pour que ce maximum soit atteint. Je veux les valeurs en millimètre arrondies à l'entier.
Remarque importante : toutes valeurs qui seront données dans la mauvaise unité ou avec la mauvaise précision ne seront pas acceptées, même si la réponse est accompagnée d'une démonstration exacte.
L=2sin/10 m soit 618mm. par défaut
l=1/(2cos/5) soit 525mm. par défaut
Je ne fais pas une grosse différence entre "valeur arrondie" et "valeur approchée" ...
Et si je donne cette consigne, c'est parce que je ne souhaite pas la valeur exacte. Ainsi, ceux qui ont une approche plus numérique que théorique peuvent aussi participer.
 salut jamo
salut jamo
tu te contredis alors avec ta " Remarque importante : "qui avait, entre autre, pour but d'éviter les remarques de ce type, sur le " souci d'équité "...

 personnellement ça m'est complètement égal que tu " n'accordes pas de différence aux "valeur arrondie" et "valeur approchée" (quoique...)
personnellement ça m'est complètement égal que tu " n'accordes pas de différence aux "valeur arrondie" et "valeur approchée" (quoique...)
c'est seulement dommage que tu aies ajouté cette " Remarque importante : " en souligné 

 Mes 6èmes non plus ne font pas une grosse différence entre valeur arrondie et valeur approchée, à mon grand désespoir...
Mes 6èmes non plus ne font pas une grosse différence entre valeur arrondie et valeur approchée, à mon grand désespoir...
Comme dit mika, c'est dommage que tu précises cela et que tu n'en tiennes pas compte, même si la réponse de veleda est tout à faire correcte, voire meilleure que les autres, comme le dit kiko ("chevauchement des sets").
 par ailleurs, au vu des participations et des résultats
par ailleurs, au vu des participations et des résultats


où l'on voit bien que kioups répond plus aux énigmes pour le fun puisqu'il participe pratiquement à toutes ( s'il jouait la place, il ne répondrait pas à certaines énigmes et, avec ses 6 réponses justes, serait en 7° place devant ITMETIC, au temps...),
Nos remarques ne sont nullement destinées à nous faire remonter dans le classement, ni à pénaliser la pôv' veleda (qui n'a rien demandé dans cette histoire  ),
),
mais bien à éviter les guéguerres qui aboutissent quelquefois ( on se souvient de Master_och, très accro à son smiley mensuel et à d'autres mathîliens ... ) à des règlements de comptes à O.K. Corral

D'autant que la remarque de jamo semblait répondre à cet objectif...

 Ce qui n'empêche pas qu'un jour, je dominerai le monde ! Enfin, pas en juillet, j'ai déjà un ou deux poissons en réserve...
Ce qui n'empêche pas qu'un jour, je dominerai le monde ! Enfin, pas en juillet, j'ai déjà un ou deux poissons en réserve...
 bonjour à tous
bonjour à tous
>>Jamo
Kioups a raison je n'ai pas donné les arrondis demandés,c'est une étourderie de ma part (j'en fait beaucoup)une fois la démonstration terminée j'ai répondu sans relire la question posée et j'ai donné des valeurs approchées
je suis tout à fait d'accord pour échanger mon smiley contre un poisson
>>Mykayaou à propos de la généralisation que tu proposes ù est la difficulté?il me semble que ma démonstration reste la même (peut être que je dis encore n'importe quoi?)
ù est la difficulté?il me semble que ma démonstration reste la même (peut être que je dis encore n'importe quoi?)
 bonjour veleda
bonjour veleda 
quand j'ai posté ma subsidiaire, je n'avais aucune connaissance de TA réponse 
je me suis dit, comme était posé l'énoncé, qu'il aurait été plus judicieux de demander la valeur exacte ( comme le demandent souvent J-P, minkus et autre puisea dans leurs énigmes ) plutôt qu'une valeur arrondie ou approchée ou ... comme le demandait jamo dans son énoncé initial ( qu'il a post-justifié après coup... )
c'est ainsi qu'en prenant le problème généralisé en (ici n = 5), j'aboutissais à :
¤ une longueur de
¤ une largeur de
¤ pour une surface de
En raisonnant en valeurs approchées, ces valeurs exactes n'étaient peut-être pas trouvées... 
Pour ceux qui on fait des analyses purement géométriques -comme toi-, leur raisonnement reste le même, et il n'y a pas de difficulté majeure
Bonnes vacances !

 Ainsi, on peut directement répondre à Dhalte
Ainsi, on peut directement répondre à Dhalte ![]() Enigmo 40 : A table ! :
Enigmo 40 : A table ! :
dhalte : Jamo, la prochaine fois, invite 16 convives. A 17, les calculs numériques seront un peu plus sportifs.

Eh bé non, dhalte, c'est tout aussi simple


Bon, reprenons les explications au sujet de cette précision demandée.
Tout d'abord, je demande une valeur exacte, ce qui permet à davantage de personnes de participer.
En effet, ceux qui ont une approche théorique vont trouver la valeur exacte, et il leur sera facile de donner la valeur approchée.
Mais d'autres préférent une approche numérique, par exemple avec Excel.
Ou même avec un logiciel du genre géogebra, je pense qu'on peut s'en sortir : on fixe les contraintes, puis en faisant bouger un point, on peut demander d'afficher l'aire du rectangle, et donc d'obtenir l'extremum.
Ensuite, si je veux une certaine précision, c'est pour éviter ce qui s'était déjà produit dans d'autres énigmes.
En effet, certains arrondissent les valeurs intermédiaires.
Ainsi, ils vont arrondir 1,4 à 1,5 puis 3,9 à 4 et à la fin ils vont me répondre 4*1,5=6 à la place de 1,4*3,9=5,46.
Donc ma remarque va dans ce sens : j'estime qu'on doit savoir aller au bout d'un calcul avec une précision donnée par rapport à la valeur exacte.
Bref, je ne comprends pas les remarques faites ...
Soyez plus clair, Jamo être bête et aimer que gens dire choses directement ! 
Nombre de participations : 0
Temps de réponse moyen : 126:01:56.




